
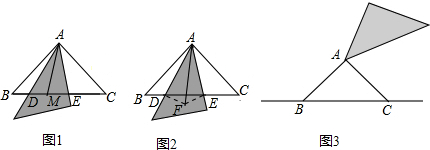
分析 (1)根据图形、已知条件推知∠BAD+∠MAE=∠DAM+∠EAC=45°,所以∠MAE=∠EAC,即AE平分∠MAC;
(2)成立.将△ABD沿AD所在的直线对折得到△ADF,连接EF,应用折叠对称的性质和SAS得到△AEF≌△AEC,在Rt△DFE中应用勾股定理而证明;
(3)当135°<α<180°时,等量关系BD2+CE2=DE2仍然成立,结论仍然成立,根据(2)的方法进行证明即可.
解答 (1)证明:
如图1,∵∠BAC=90°,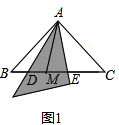
∴∠BAD+∠DAM+∠MAE+∠EAC=90°.
∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∵∠BAD=∠DAM,
∴∠BAD+∠EAC=∠DAM+∠EAC=45°,
∴∠BAD+∠MAE=∠DAM+∠EAC,
∴∠MAE=∠EAC,
即AE平分∠MAC;
(2)证明:
如图2,将△ABD沿AD所在的直线对折得到△ADF,连接EF.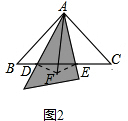
由折叠可知,∠BAD=∠FAD,AB=AF,BD=DF,
∴AF=AC,
又由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中
$\left\{\begin{array}{l}{AF=AC}\\{∠FAE=∠CAE}\\{AE=AE}\end{array}\right.$
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°,
∴∠DFE=∠AFD+∠AFE=90°,
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2,
即线段BD、CE、DE这三条线段可以围成以DE为斜边的直角三角形;
(3)当135°<α<180°时,线段BD、CE、DE是否仍能围成以DE为斜边的直角三角形.
证明如下:
如图3,将△ABD沿AD所在的直线对折得到△ADF,连接EF,设AB与EF相交于点G,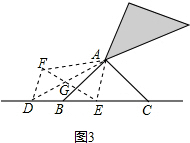
∵将△ABD沿AD所在的直线对折得到△ADF,
∴AF=AB,∠AFD=∠ABD=135°,∠BAD=∠FAD,
又∵AC=AB,
∴AF=AC,
又∵∠CAE=90°-∠BAE=90°-(45°-∠BAD)=45°+∠BAD=45°+∠FAD=∠FAE,
∴∠CAE=∠FAE,
在△AEF和△AEC中,
∵$\left\{\begin{array}{l}{AF=AC}\\{∠FAE=∠CAE}\\{AE=AE}\end{array}\right.$,
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°,
∴∠DFE=∠AFD-∠AFE=∠135°-∠C=135°-45°=90°,
∴∠DFE=90°,
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2,
即线段BD、CE、DE是否仍能围成以DE为斜边的直角三角形.
点评 本题考查了几何变换综合性题目,用到的知识点有角平分线的定义,等腰直角三角形的性质,旋转的性质,折叠对称的性质,全等三角形的判定和性质等,题目的综合性较强,难度较大,正确做出图形的辅助线是解题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为110.
在我国古算书《周髀算经》中记载周公与商高的谈话,其中就有勾股定理的最早文字记录,即“勾三股四弦五”,亦被称作商高定理.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,则D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为110.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,$\sqrt{2}$,4 | B. | 4,5,6 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a$≤\frac{17}{2}$ | B. | a≤12 | C. | a<$\frac{17}{2}$ | D. | a<12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com