Question

【题目】已知∠MON=90°，线段AB长为6cm，AB两端分别在OM、ON上滑动，以AB为边作正方形ABCD，对角线AC、BD相交于点P，连结OC．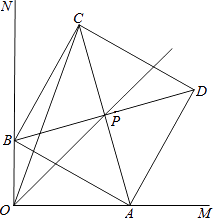

（1）求证：无论点A、点B怎样运动，点P都在∠AOB的平分线上；
（2）若OP=4 ，求OA的长．
（3）求OC的最大值（提示：取AB的中点Q，连接CQ、OQ，运用两点之间，线段最短）

Answer 1

【答案】
（1）

解：如图，作PE⊥OM、PF⊥ON垂足分别为E、F，

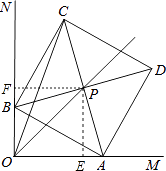
则∠PEA=∠PFB=90°=∠EOF，

∴∠EPF=90°，

∵ABCD是正方形，

∴PA=PB，且∠APB=90°，

∴∠APE+∠BPE=∠BPF+∠BPE，

即∠APE=∠BPF，

在△AEP和△BFP中，

，

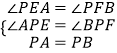∴△PAE≌△PBF（AAS），

∴PE=PF，

即点P在∠AOB的平分线上

（2）

解：∵四边形OEPF是正方形，OP=4 ，

∴OE=PE=4，

又∵Rt△APB中，AB=6，

∴PA=3 ，

∴Rt△AEP中，AE= = ，

∴OA=OE+AE=4+ 或OA=OE﹣AE=4﹣

（3）

解：如图，取AB的中点Q，连接OQ，CQ，OC，

∵AB长度不变，BC长度不变，

∴Rt△AOB中，OQ= AB=3，

Rt△BCQ中，CQ= =3 ，

∵OQ+CQ≥OC，

∴当O，C，Q三点共线时，OC有最大值，

OC最大值=OQ+QC=3+3 ．

【解析】（1）作PE⊥OM、PF⊥ON垂足分别为E、F，根据AAS判定△PAE≌△PBF，即可得出PE=PF，进而得到点P在∠AOB的平分线上；（2）根据四边形OEPF是正方形，OP=4 ，可得OE=PE=4，再根据Rt△APB中，AB=6，可得PA=3 ，进而得到Rt△AEP中，AE= ，据此可得OA的长；（3）取AB的中点Q，连接OQ，CQ，OC，根据AB长度不变，BC长度不变，可得Rt△AOB中，OQ= AB=3，Rt△BCQ中，CQ=3 ，再根据OQ+CQ≥OC，可得当O，C，Q三点共线时，OC有最大值，进而得到OC最大值=OQ+QC=3+3 ．