
【题目】如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE. 求证:四边形BCDE是矩形.
【答案】证明:∵∠BAD=∠CAE, ∴∠BAD﹣∠BAC=∠CAE﹣∠BAC,
∴∠BAE=∠CAD,
∵在△BAE和△CAD中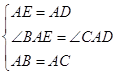
∴△BAE≌△CAD(SAS),
∴∠BEA=∠CDA,BE=CD,
∵DE=CB,
∴四边形BCDE是平行四边形,
∵AE=AD,
∴∠AED=∠ADE,
∵∠BEA=∠CDA,
∴∠BED=∠CDE,
∵四边形BCDE是平行四边形,
∴BE∥CD,
∴∠CDE+∠BED=180°,
∴∠BED=∠CDE=90°,
∴四边形BCDE是矩形.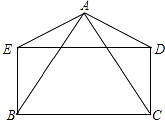
【解析】求出∠BAE=∠CAD,证△BAE≌△CAD,推出∠BEA=∠CDA,BE=CD,得出平行四边形BCDE,根据平行线性质得出∠BED+∠CDE=180°,求出∠BED,根据矩形的判定求出即可.


科目:初中数学 来源: 题型:
【题目】已知△ABC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空: 
(1)作∠ABC的平分线BD交AC于点D;
(2)作线段BD的垂直平分线交AB于点E,交BC于点F.由(1)、(2)可得:线段EF与线段BD的关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)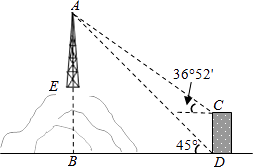
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F. 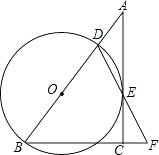
(1)求证:BD=BF;
(2)若CF=1,cosB= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,且m﹣n+2≠0,则当x=3(m+n+1)时,多项式x2+4x+6的值等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设边长为3的正方形的对角线长为a.下列关于a的四种说法: ①a是无理数;
②a可以用数轴上的一个点来表示;
③3<a<4;
④a是18的算术平方根.
其中,所有正确说法的序号是( )
A.①④
B.②③
C.①②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表: 
(1)理解划线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;
(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图; 
(3)该校数学兴趣小组结合调查获取信息,向学校提出了一些建议,如:骑车上学的学生约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8). 绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
(1)E类学生有人,补全条形统计图;
(2)D类学生人数占被调查总人数的%;
(3)从该班做义工时间在0≤t≤4的学生中任选2人,求这2人做义工时间都在2<t≤4中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com