
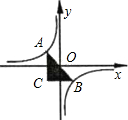
 如图中直角△ABC面积为8,则图中双曲线的解析式是
如图中直角△ABC面积为8,则图中双曲线的解析式是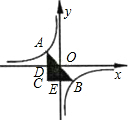 解:设反比例函数的解析式为y=
解:设反比例函数的解析式为y=| k |
| x |
| k |
| x |
| k |
| x |
| k |
| x |
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| x |
| 4 |
| x |


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
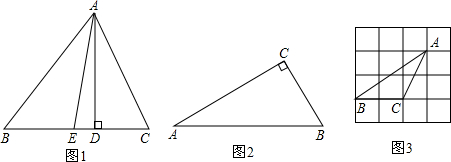
 如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.
如图,有一块直角三角形土地,它两条直角边AB=300米,AC=400米,某单位要沿着斜边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上,设EF为x,矩形面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平 面直角坐标系.
如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平 面直角坐标系.| 13 |
| 3 |
| 11 |
| 2 |
| 13 |
| 3 |
| 11 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| DE | BE |
查看答案和解析>>
科目:初中数学 来源:2012届河北省保定市易县九年级第一次模拟检测数学试卷(带解析) 题型:解答题
如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B (-1,0)、A (0,2),AC⊥AB.
(1)求线段OC的长;
(2)点P从B点出发以每秒4个单位的速度沿x轴正半轴运动,点Q从A点出发沿线段AC以每秒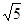 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面 积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
(3)Q点沿射线AC按原速度运动,⊙G过A、B、Q三点,是否有这样的t值使点P在⊙G上、如果有求t值,如果没有说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河北省保定市易县九年级第一次模拟检测数学试卷(解析版) 题型:解答题
如图,Rt△ABC在平面直角坐标系中,BC在x轴上,B (-1,0)、A (0,2),AC⊥AB.

(1)求线段OC的长;
(2)点P从B点出发以每秒4个单位的速度沿x轴正半轴运动,点Q从A点出发沿线段AC以每秒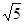 个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
个单位的速度向点C运 动,当一点停止运动,另一点也随之停止,设△CPQ的面
积为S,两点同时运动,运动的时间为t秒,求S与t之间关系式,并写出自变量取值范围;
(3)Q点沿射线AC按原速度运动,⊙G过A、B、Q三点,是否有这样的t值使点P在⊙G上、如果有求t值,如果没有说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com