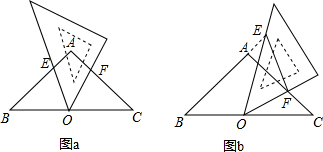
(1)证明:∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BOE+∠BEO=180°,
∴∠BOE+∠BEO=135°,
∵∠EOF=45°,
又∵∠BOE+∠EOF+∠COF=180°,
∴∠BOE+∠COF=135°,
∴∠BEO=∠COF,
又∵∠B=∠C,
∴△BOE∽△CFO(两角对应相等的两个三角形相似).
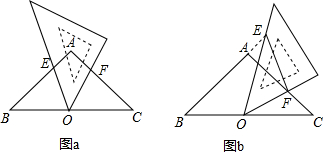
(2)解:①△BOE∽△CFO;②△BOE与△OFE相似.
证明:同(1),可证△BOE∽△CFO,
得 CO:BE=OF:OE,
而CO=BO,
因此 OB:BE=OF:OE.
又因为∠EBO=∠EOF,
所以△BOE∽△OFE(两边对应成比例且夹角相等的两个三角形相似).
②△ABC为等腰直角三角形,且AB=AC=2,O为BC中点,
∴BO=

.
设EO=y,
∵△BOE∽△OFE,
∴
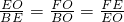
,
即
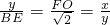
,
解得:FO=
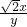
,
则S
△EOF=

•sin45°•EO•FO=

•EO•FO.
∵EO•FO=

x.
∴S=

x.
分析:(1)找出△BOE与△CFO的对应角,其中∠BOE+∠COF=135°,∠COF+∠CFO=135°,得出∠BOE=∠CFO,从而解决问题;
(2)①小题同前可证,②小题可通过对应边成比例证明.
点评:此题主要考查了相似三角形的判定.它以每位学生都有的三角板在图形上的运动为背景,既考查了学生图形旋转变换的思想,静中思动,动中求静的思维方法,又考查了学生动手实践、自主探究的能力.


 .
.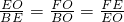 ,
,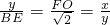 ,
,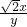 ,
, •sin45°•EO•FO=
•sin45°•EO•FO= •EO•FO.
•EO•FO. x.
x. x.
x.

 阅读快车系列答案
阅读快车系列答案 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°, ,连接AO、BE、DC.
,连接AO、BE、DC.