
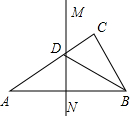
 如图所示,直线MN∥BC,AD⊥BC,垂足为D,∠MAB=∠NAC,求∠1与∠2的大小关系如何?请说明理由.
如图所示,直线MN∥BC,AD⊥BC,垂足为D,∠MAB=∠NAC,求∠1与∠2的大小关系如何?请说明理由.科目:初中数学 来源: 题型:

| 4 |
| n |
| 4 |
| n |
查看答案和解析>>
科目:初中数学 来源:2012届浙江省江山市中考一模数学试卷(带解析) 题型:解答题
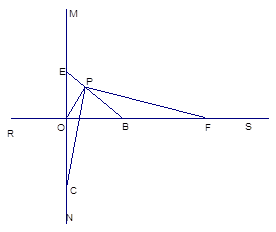
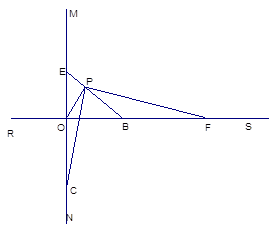
如图所示:直线MN⊥RS于点O,点B在射线OS上,OB=2,点C在射线ON上,OC=2,点E是射线OM上一动点,连结EB,过O作OP⊥EB于P,连结CP,过P作PF⊥PC交射线OS于F。
(1)求证:△POC∽△PBF。
(2)当OE=1,OE=2时, BF的长分别为多少?当OE=n时,BF=_______.
(3)当OE=1时,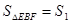 ;OE=2时,
;OE=2时,  ;…,OE=n时,
;…,OE=n时,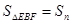 .则
.则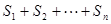 =_______.(直接写出答案)
=_______.(直接写出答案)
|
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省江山市中考一模数学试卷(解析版) 题型:解答题
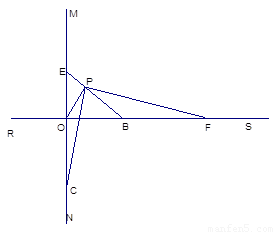
如图所示:直线MN⊥RS于点O,点B在射线OS上,OB=2,点C在射线ON上,OC=2,点E是射线OM上一动点,连结EB,过O作OP⊥EB于P,连结CP,过P作PF⊥PC交射线OS于F。
(1)求证:△POC∽△PBF。
(2)当OE=1,OE=2时, BF的长分别为多少?当OE=n时,BF=_______.
(3)当OE=1时, ;OE=2时,
;OE=2时,  ;…,OE=n时,
;…,OE=n时,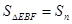 .则
.则 =_______.(直接写出答案)
=_______.(直接写出答案)
|

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com