
如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC,OE=![]() BC.
BC.
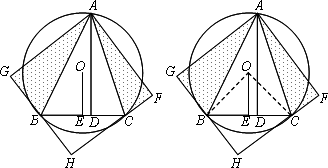
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
|
(1)解:连结OB和OC. ∵OE⊥BC,∴BE=CE. ∵OE= (2)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°. 由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°, ∠BAG=∠BAD,∠CAF=∠CAD, (3分) ∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°. ∴∠GAF=∠BAG+∠CAF+∠BAC=90°. ∴四边形AFHG是正方形. (5分) (3)解:由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4. 设AD的长为x,则BH=GH-GB=x-6,CH=HF-CF=x-4. (7分) 在Rt△BCH中,BH2+CH2=BC2,∴(x-6)2+(x-4)2=102. 解得,x1=12,x2=-2(不合题意,舍去). ∴AD=12. (8分) |


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com