
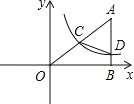
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
【答案】(1)反比例函数解析式为:y=![]() ;
;
(2)![]()
【解析】
试题分析:(1)先根据锐角三角函数的定义,求出OA的值,然后根据勾股定理求出AB的值,然后由C点是OA的中点,求出C点的坐标,然后将C的坐标代入反比例函数y=![]() 中,即可确定反比例函数解析式;
中,即可确定反比例函数解析式;
(2)先将y=3x与y=![]() 联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
联立成方程组,求出点M的坐标,然后求出点D的坐标,然后连接BC,分别求出△OMB的面积,△OBC的面积,△BCD的面积,进而确定四边形OCDB的面积,进而可求三角形OMB与四边形OCDB的面积的比.
试题解析:(1)∵A点的坐标为(8,y),∴OB=8,∵AB⊥x轴于点B,sin∠OAB=![]() ,
,
∴![]() ,∴OA=10,由勾股定理得:AB=
,∴OA=10,由勾股定理得:AB=![]() ,
,
∵点C是OA的中点,且在第一象限内,∴C(4,3),∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴k=12,∴反比例函数解析式为:y=![]() ;
;
(2)将y=3x与y=![]() 联立成方程组,得:
联立成方程组,得: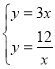 ,
,
解得: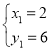 ,
, ,
,
∵M是直线与双曲线另一支的交点,∴M(﹣2,﹣6),∵点D在AB上,∴点D的横坐标为8,
∵点D在反比例函数y=![]() 的图象上,∴点D的纵坐标为
的图象上,∴点D的纵坐标为![]() ,∴D(8,
,∴D(8,![]() ),∴BD=
),∴BD=![]() ,
,
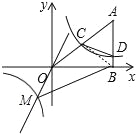
连接BC,如图所示,∵S△MOB=![]() 8|﹣6|=24,S四边形OCDB=S△OBC+S△BCD=
8|﹣6|=24,S四边形OCDB=S△OBC+S△BCD=![]() 83+
83+![]() =15,
=15,
∴![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
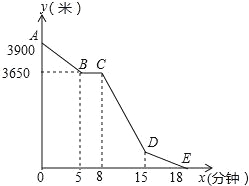
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
(1)小丽步行的速度为 ;
(2)写出y与x之间的函数关系式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用等式的性质进行变形时,下列各式中,不一定正确的是( )
A. 如果a=b,那么a-c=b-c B. 如果a=b,那么a+c=b+c
C. 如果a=b,那么ab=ac D. 如果a=b,那么ac=bc
查看答案和解析>>
科目:初中数学 来源: 题型:
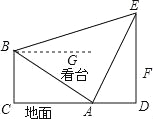
【题目】如图所示,体育场内一看台与地面所成夹角为30°,看台最低点A到最高点B的距离为10![]() ,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
,A,B两点正前方有垂直于地面的旗杆DE.在A,B两点处用仪器测量旗杆顶端E的仰角分别为60°和15°(仰角即视线与水平线的夹角)
(1)求AE的长;
(2)已知旗杆上有一面旗在离地1米的F点处,这面旗以0.5米/秒的速度匀速上升,求这面旗到达旗杆顶端需要多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com