
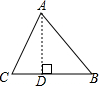
 ��ͼ���ڡ�ABC�У�AB=15��BC=14��AC=13�����ABC�������
��ͼ���ڡ�ABC�У�AB=15��BC=14��AC=13�����ABC����������� ��1��ֱ������BC�ij���ʾ��DC�ij���
��2��ֱ�����ù��ɶ��������ó�x��ֵ��
��3����������������ó��𰸣�
��� �⣺��1����BC=14��BD=x��
��DC=14-x��
�ʴ�Ϊ��14-x��
��2����AD��BC��
��AD2=AC2-CD2��AD2=AB2-BD2��
��132-��14-x��2=152-x2��
��ã�x=9��
��3���ɣ�2���ã�AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{1{5}^{2}-{9}^{2}}$=12��
��S��ABC=$\frac{1}{2}$•BC•AD=$\frac{1}{2}$��14��12=84��
���� ������Ҫ�����˹��ɶ����Լ��������������ȷ�ó�AD�ij��ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��Ц����ס�ĵ���������Ϊ��������
��ͼ��Ц����ס�ĵ���������Ϊ��������| A�� | ��5��2�� | B�� | ��-4��-6�� | C�� | ��3��-4�� | D�� | ��-2��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����x��Գ� | B�� | ����y��Գ� | ||
| C�� | ����ֱ��x=-1�Գ� | D�� | ����ֱ��y=-1�Գ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
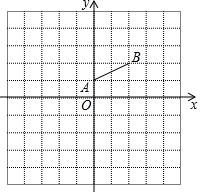 ��ͼ���������������У�ÿ��С�����εı߳�Ϊ1����λ���ȣ�ƽ��ֱ������ϵxOy��ԭ��O�ڸ���ϣ�x�ᡢy�ᶼ�ڸ����ϣ��߶�AB�������˵�Ҳ�ڸ���ϣ�
��ͼ���������������У�ÿ��С�����εı߳�Ϊ1����λ���ȣ�ƽ��ֱ������ϵxOy��ԭ��O�ڸ���ϣ�x�ᡢy�ᶼ�ڸ����ϣ��߶�AB�������˵�Ҳ�ڸ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
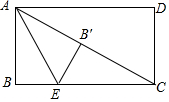 ��ͼ������ABCD�У�AB=5��BC=10����EΪ��BC��һ���㣬�ѡ�ABE��AE�۵�����B����B������B��ǡ�����ھ���ABCD�ĶԽ�����ʱ��BE�ij�Ϊ$\frac{5\sqrt{5}}{2}$-$\frac{5}{2}$��
��ͼ������ABCD�У�AB=5��BC=10����EΪ��BC��һ���㣬�ѡ�ABE��AE�۵�����B����B������B��ǡ�����ھ���ABCD�ĶԽ�����ʱ��BE�ij�Ϊ$\frac{5\sqrt{5}}{2}$-$\frac{5}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
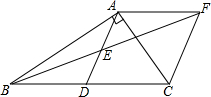 ��ͼ���ڡ�ABC�У���BAC=90�㣬AD�����ߣ�E��AD���е㣬����A��AF��BC��BE���ӳ�����F������CF����֤���ı���ADCF�����Σ�
��ͼ���ڡ�ABC�У���BAC=90�㣬AD�����ߣ�E��AD���е㣬����A��AF��BC��BE���ӳ�����F������CF����֤���ı���ADCF�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
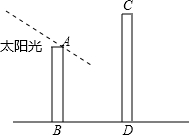 ��ͼ��ABΪijһС���ڵľ���¥����Ϊ18�ף�Ϊ����ס�����ŵ�״�����־������ⶰ����¥�����һ����¥��ͼ��CD��������һ¥��6�ߵ�С�����У���̫������ˮƽ�ߵļн�Ϊ30��ʱ��
��ͼ��ABΪijһС���ڵľ���¥����Ϊ18�ף�Ϊ����ס�����ŵ�״�����־������ⶰ����¥�����һ����¥��ͼ��CD��������һ¥��6�ߵ�С�����У���̫������ˮƽ�ߵļн�Ϊ30��ʱ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com