
分析 (1)依据多项式乘多项式进行计算,然后合并同类项即可;
(2)依据(1)中的计算找出其中的规律,最后,依据规律进行计算即可;
(3)依据(1)中的计算规律得到原式=22015-1,然后找出2的正整数次幂的个位数的规律,最后依据规律解答即可.
解答 解:(1)②(x-1)(x2+x+1)=x3+x2+x-x2-x-1=x3-1;
③(x-1)(x3+x2+x+1)=x4+x3+x2+x-x3-x2-x-1=x4-1;
④(x-1)(x4+x3+x2+x+1)=x5+x4+x3+x2+x-x4-x3-x2-x-1=x5-1;
(2)26+25+24+23+22+2+1=(2-1)(26+25+24+23+22+2+1)=27-1=127
(3)22014+22013+22012+…+22+2+1=(2-1)(22014+22013+22012+…+22+2+1)=22015-1.
∵21=2,22=4,23=8,24=16,25=32,26=64,
∴22015的个位数为8,
∴22015-1的个位数为7.
点评 本题主要考查的是多项式乘多项式找出其中的规律是解题的关键.


科目:初中数学 来源: 题型:选择题
 “龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法:
“龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
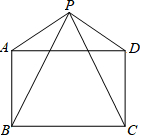 如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.
如图,四边形ABCD中,AD=BC,P是四边形ABCD外一点,且PA=PD,PB=PC,∠APB=∠DPC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
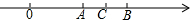 如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )
如图,数轴上点C和点B分别表示2和$\sqrt{5}$,若点C是AB的中点,点A表示的实数为( )| A. | 2-$\sqrt{5}$ | B. | 4-$\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $\sqrt{5}$-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
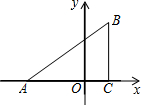 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.
已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),$\frac{BC}{AC}$=$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com