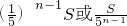
分析:由E、F、G、H分别为菱形A
1B
1C
1D
1各边的中点,得到A
1H=C
1F,又A
1H∥C
1F,利用一组边长平行且相等的四边形为平行四边形得到四边形A
1HC
1F为平行四边形,根据平行线间的距离相等及平行四边形与三角形的面积公式,可得出四边形A
1HC
1F的面积等于△HB
1C
1面积的2倍,等于△A
1D
1F面积的2倍,而这三个的面积之和为菱形的面积S,可得出四边形A
1HC
1F面积为菱形面积S的一半,再由平行线等分线段定理得到A
2为A
1D
2的中点,C
2为C
1B
2的中点,B
2为B
1A
2的中点,D
2为D
1C
2的中点,利用三角形的中位线定理得到HB
2=

A
1A
2,D
2F=

C
1C
2,可得出A
1A
2B
2H和C
1C
2D
2F都为梯形,且高与平行四边形A
2B
2C
2D
2的高h相等(设高为h),下底与平行四边形A
2B
2C
2D
2的边A
2D
2与x相等(设A
2D
2=x),分别利用梯形的面积公式及平行四边形的面积公式表示出各自的面积,得出三个面积之比,可得出平行四边形A
2B
2C
2D
2的面积占三个图形面积的

,即为四边形A
1HC
1F面积的

,为菱形面积的

,同理得到四边形A
3B
3C
3D
3的面积为菱形面积的(

)
2,以此类推,表示出四边形A
nB
nC
nD
n的面积即可.
解答:∵H为A
1B
1的中点,F为C
1D
1的中点,
∴A
1H=B
1H,C
1F=D
1F,
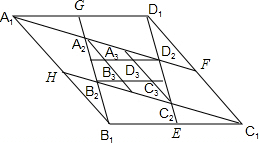
又A
1B
1C
1D
1为菱形,∴A
1B
1=C
1D
1,
∴A
1H=C
1F,又A
1H∥C
1F,
∴四边形A
1HC
1F为平行四边形,
∴S
四边形A1HC1F=2S
△HB1C1=2S
△A1D1F,
又S
四边形A1HC1F+S
△HB1C1+S
△A1D1F=S
菱形A1B1C1D1=S,
∴S
四边形A1HC1F=

S,
又GD
1=B
1E,GD
1∥B
1E,
∴GB
1ED
1为平行四边形,
∴GB
1∥ED
1,又G为A
1D
1的中点,
∴A
2为A
1D
2的中点,
同理C
2为C
1B
2的中点,B
2为B
1A
2的中点,D
2为D
1C
2的中点,
∴HB
2=

A
1A
2,D
2F=

C
1C
2,
又A
1A
2B
2H和C
1C
2D
2F都为梯形,且高与平行四边形A
2B
2C
2D
2的高h相等(设高为h),
下底与平行四边形A
2B
2C
2D
2的边A
2D
2与x相等(设A
2D
2=x),
∴S
梯形A1A2B2H=S
梯形C1C2D2F=

(x+

x)h=

xh,S
平行四边形A2B2C2D2=xh,
即S
梯形A1A2B2H:S
梯形C1C2D2F:S
平行四边形A2B2C2D2=3:3:4,
又S
梯形A1A2B2H+S
梯形C1C2D2F+S
平行四边形A2B2C2D2=S
四边形A1HC1F,
∴S
平行四边形A2B2C2D2=

S
四边形A1HC1F=

S,
同理S
四边形A3B3C3D3=(

)
2S,
以此类推得四边形A
nB
nC
nD
n的面积为(

)
n-1S或
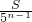
.
故答案为:(

)
n-1S或
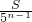
.
点评:此题考查了三角形的中位线定理,平行四边形的判定与性质,平行线等分线段定理,以及平行四边形与三角形面积的计算,利用了转化的数学思想,是一道规律型试题,灵活运用三角形中位线定理是解本题的关键.

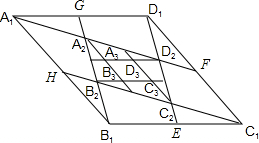 如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为________.
如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为________.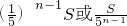
 A1A2,D2F=
A1A2,D2F= C1C2,可得出A1A2B2H和C1C2D2F都为梯形,且高与平行四边形A2B2C2D2的高h相等(设高为h),下底与平行四边形A2B2C2D2的边A2D2与x相等(设A2D2=x),分别利用梯形的面积公式及平行四边形的面积公式表示出各自的面积,得出三个面积之比,可得出平行四边形A2B2C2D2的面积占三个图形面积的
C1C2,可得出A1A2B2H和C1C2D2F都为梯形,且高与平行四边形A2B2C2D2的高h相等(设高为h),下底与平行四边形A2B2C2D2的边A2D2与x相等(设A2D2=x),分别利用梯形的面积公式及平行四边形的面积公式表示出各自的面积,得出三个面积之比,可得出平行四边形A2B2C2D2的面积占三个图形面积的 ,即为四边形A1HC1F面积的
,即为四边形A1HC1F面积的 ,为菱形面积的
,为菱形面积的 ,同理得到四边形A3B3C3D3的面积为菱形面积的(
,同理得到四边形A3B3C3D3的面积为菱形面积的( )2,以此类推,表示出四边形AnBnCnDn的面积即可.
)2,以此类推,表示出四边形AnBnCnDn的面积即可. 又A1B1C1D1为菱形,∴A1B1=C1D1,
又A1B1C1D1为菱形,∴A1B1=C1D1, S,
S, A1A2,D2F=
A1A2,D2F= C1C2,
C1C2, (x+
(x+ x)h=
x)h= xh,S平行四边形A2B2C2D2=xh,
xh,S平行四边形A2B2C2D2=xh, S四边形A1HC1F=
S四边形A1HC1F= S,
S, )2S,
)2S, )n-1S或
)n-1S或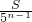 .
. )n-1S或
)n-1S或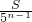 .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2