
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m-3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
【答案】(1)18;(2)有6种购买方案,每月最多处理污水量的吨数为2000吨.
【解析】
试题分析:(1)根据90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,列出m的分式方程,求出m的值即可;
(2)设买A型污水处理设备x台,B型则(10-x)台,根据题意列出x的一元一次不等式,求出x的取值范围,进而得出方案的个数,并求出最大值.
试题解析:(1)由90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,
即可得:![]() ,
,
解得m=18,
经检验m=18是原方程的解,即m=18;
(2)设买A型污水处理设备x台,则B型(10-x)台,
根据题意得:18x+15(10-x)≤165,
解得x≤5,由于x是整数,则有6种方案,
当x=0时,10-x=10,月处理污水量为1800吨,
当x=1时,10-x=9,月处理污水量为220+180×9=1840吨,
当x=2时,10-x=8,月处理污水量为220×2+180×8=1880吨,
当x=3时,10-x=7,月处理污水量为220×3+180×7=1920吨,
当x=4时,10-x=6,月处理污水量为220×4+180×6=1960吨,
当x=5时,10-x=5,月处理污水量为220×5+180×5=2000吨,
答:有6种购买方案,每月最多处理污水量的吨数为2000吨.


科目:初中数学 来源: 题型:
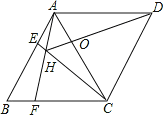
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD2=ODDH中,正确的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
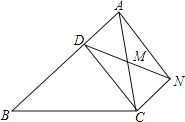
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查方式的是( )
A. 对乌达区中学生心理健康现状的调查
B. 对冷饮市场上冰淇淋质量情况的调查
C. 审核书稿中的错别字
D. 调查乌达区中学生社会主义核心价值观的背诵情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种面粉的质量标识为“26±0.25千克”,则下列面粉中合格的是:( )
A. 26.30千克 B. 25.70千克 C. 26.51千克 D. 25.80千克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com