
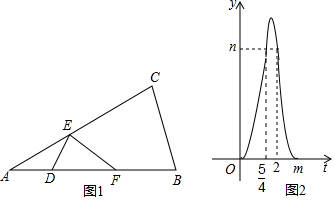
分析 (1)如图1中,作CK⊥AB于K,EH⊥AB于H.由题意AC=AB=8,当点F与点B重合时,AE=EB=5,在Rt△EHB中,HB=4,EB=5,EH=$\sqrt{E{B}^{2}-B{H}^{2}}$=3,设AD=DE=x,在Rt△EDH中,由DE2=EH2+DH2,可得x2=32+(4-x)2,可得x=$\frac{25}{8}$,推出DH=AH-AD=$\frac{7}{8}$,推出n=S△EDB=$\frac{1}{2}$•DB•EH=$\frac{1}{2}$•(4+$\frac{7}{8}$)•3=$\frac{117}{16}$,当AE=4t时,易知AD=DE=$\frac{5}{4}$•2t=$\frac{5}{2}$t,可得$\frac{5}{2}$t=8,推出t=$\frac{16}{5}$,即m=$\frac{16}{5}$.
(2)分三种情形分别求解即可.
解答 解:(1)如图1中,作CK⊥AB于K,EH⊥AB于H.
由题意AC=AB=8,当点F与点B重合时,AE=EB=5,
在Rt△EHB中,HB=4,EB=5,EH=$\sqrt{E{B}^{2}-B{H}^{2}}$=3,设AD=DE=x,
在Rt△EDH中,∵DE2=EH2+DH2,
∴x2=32+(4-x)2,
∴x=$\frac{25}{8}$,
∴DH=AH-AD=$\frac{7}{8}$,
∴n=S△EDB=$\frac{1}{2}$•DB•EH=$\frac{1}{2}$•(4+$\frac{7}{8}$)•3=$\frac{117}{16}$,
当AE=4t时,易知AD=DE=$\frac{5}{4}$•2t=$\frac{5}{2}$t,
∴$\frac{5}{2}$t=8,
∴t=$\frac{16}{5}$,
∴m=$\frac{16}{5}$.
故答案为$\frac{16}{5}$,$\frac{117}{16}$.
(2)①当0≤t≤$\frac{5}{4}$,如图2中,重叠部分是△DEF.易知AD=DE=$\frac{5}{2}$t,AH=HF=$\frac{4}{5}$•4t=$\frac{16}{5}$t,EH=$\frac{3}{5}$•4t=$\frac{12}{5}$t,DH=AH-AD=$\frac{7}{10}$t,DF=DH+HF=$\frac{39}{10}$t,
∴y=$\frac{1}{2}$•DF•EH=$\frac{1}{2}$$•\frac{39}{10}$t•$\frac{12}{5}$t=$\frac{117}{25}$t2,
②当$\frac{5}{4}$<t≤2,如图3中,重叠部分是四边形DEMB,作BE′∥EF交AC于E′,作BN⊥AC于N,则易知BK=CK=$\frac{24}{5}$,S△BCE′=$\frac{1}{2}$•3•$\frac{24}{5}$=$\frac{36}{5}$,
∵△CEM∽△CE′B,
∴$\frac{{S}_{△CEM}}{{S}_{△CE′B}}$=($\frac{CE}{CE′}$)2,
∴S△CEM=$\frac{36}{5}$•($\frac{8-4t}{3}$)2,
∴y=S△ABC-S△CEM=$\frac{1}{2}$•8•$\frac{24}{5}$-$\frac{36}{5}$•($\frac{8-4t}{3}$)2=-$\frac{64}{5}$t2+$\frac{264}{5}$t-$\frac{168}{5}$.
③当2<t≤$\frac{16}{5}$时如图4中,重叠部分是△DMB.作CH∥ED交AB于H.易知AH=CH=5,HB=3,S△CHB=$\frac{1}{2}$•3•$\frac{24}{5}$=$\frac{36}{5}$,
∵△MDB∽△CHB,
∴$\frac{{S}_{△MDB}}{{S}_{△CHB}}$=($\frac{DB}{HB}$)2=($\frac{8-\frac{5}{2}t}{3}$)2,
∴y=$\frac{36}{5}$•($\frac{8-\frac{5}{2}t}{3}$)2=5t2-32t+$\frac{256}{5}$.
综上所述,y=$\left\{\begin{array}{l}{\frac{117}{25}{t}^{2}}&{(0≤t≤\frac{5}{4})}\\{-\frac{64}{5}{t}^{2}+\frac{264}{5}t-\frac{168}{5}}&{(\frac{5}{4}<t≤2)}\\{5{t}^{2}-32t+\frac{256}{5}}&{(2<t≤\frac{16}{5})}\end{array}\right.$.
点评 本题考查动点问题综合题、等腰三角形的性质、三角形的面积、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会看懂图象信息,学会用分类讨论分思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
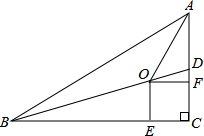 如图,Rt△ABC中,∠C=90°,∠ABC=40°,BD是△ABC的一条角平分线,点D、F、E分别在AC、BC上,O在BD上,且四边形CEOF是正方形,则∠AOD的度数是( )
如图,Rt△ABC中,∠C=90°,∠ABC=40°,BD是△ABC的一条角平分线,点D、F、E分别在AC、BC上,O在BD上,且四边形CEOF是正方形,则∠AOD的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
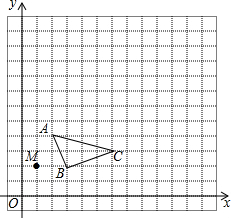 已知:△ABC和点M(1,2),
已知:△ABC和点M(1,2),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
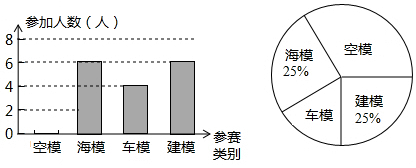
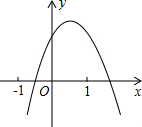 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②c>0;③a-b+c<0;④b2-4ac>0,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①a<0;②c>0;③a-b+c<0;④b2-4ac>0,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com