
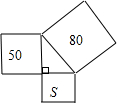
 如图,则小正方形的面积S=________.
如图,则小正方形的面积S=________. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:044
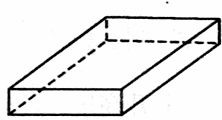
用一块边长为60 cm的正方形薄铁片制作一个长方体的盒子.
(1)如果要做成没有盖的盒子,可先在薄铁片的四个角上截去四个相同的小正方形(如图),然后把四边折合起来.

①求做成的盒子如图,则这个盒子的底面积![]() 与截去小正方形边长x(cm)的函数关系式;
与截去小正方形边长x(cm)的函数关系式;
②当做成盒子的底面积为![]() 时,求盒子的容积.
时,求盒子的容积.
(2)若要做成有盖的盒子,要满足两个条件:
①必须在四个角上各截去一个四边形,其余部分不能裁截;
②折合后薄片既无缝隙又不重叠地围成各盒面,请画出制作方案的一种草图(不必加说明与画法).
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市九年级上学期期中考试数学卷 题型:填空题
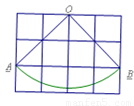
如图,扇形OAB是圆锥的侧面展开图,若小正方形的边长均为1cm,则这个圆锥的底面圆的半径为 cm。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com