
如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(![]() )时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
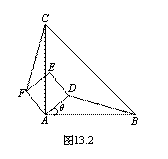
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
① 求证:BD⊥CF;
② 当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.
 |
图1 图2 图3
解(1)BD=CF成立.
理由:∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=![]() ,∠CAF=
,∠CAF=![]() ,
,
 ∴∠BAD=∠CAF,∴△BAD≌△CAF.
∴∠BAD=∠CAF,∴△BAD≌△CAF.
∴BD=CF.
(2)①证明:设BG交AC于点M.
∵△BAD≌△CAF(已证),∴∠ABM=∠GCM.
∵∠BMA =∠CMG ,∴△BMA ∽△CMG.
∴∠BGC=∠BAC =90°.∴BD⊥CF.
)
 ②过点F作FN⊥AC于点N.
②过点F作FN⊥AC于点N.
∵在正方形ADEF中,AD=![]() ,
,
∴AN=FN=![]() .
.
∵在等腰直角△ABC 中,AB=4,
∴CN=AC-AN=3,BC=![]() .
.
Rt△FCN∽Rt△ABM,∴![]()
∴AM=![]()
![]() .
.
∴CM=AC-AM=4-![]() =
=![]() ,
,![]() .
.
∵△BMA ∽△CMG,∴![]() .
.
∴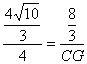 . ∴CG=
. ∴CG=![]() .
.
∴在Rt△BGC中,![]()
![]() .)
.)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com