
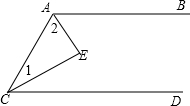
 如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E为多少?
如图,AB∥CD,AE平分∠BAC,CE平分∠ACD,求∠E为多少? ∠ACD (原因:________)
∠ACD (原因:________) ∠CAB(原因:________)
∠CAB(原因:________) (∠CAB+∠ACD)=90°(等量代换)
(∠CAB+∠ACD)=90°(等量代换) ∠ACD,∠2=∠BAE=
∠ACD,∠2=∠BAE= ∠CAB,再根据平行线的性质得出∠CAB+∠ACD=180°,利用三角形内角和定理即可得出答案.
∠CAB,再根据平行线的性质得出∠CAB+∠ACD=180°,利用三角形内角和定理即可得出答案. ∠ACD (角平分线的定义),
∠ACD (角平分线的定义), ∠CAB(原因:角平分线的定义),
∠CAB(原因:角平分线的定义), (∠CAB+∠ACD)=90°(等量代换),
(∠CAB+∠ACD)=90°(等量代换),

 智慧小复习系列答案
智慧小复习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com