
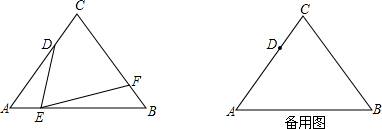
分析 (1)构造直角三角形,利用特殊角的三角函数值得出答案即可;
(2)①由∠ADE+∠AED=120°和∠BEF+∠AED=120°推出∠ADE=∠BEF,证出△ADE∽△BEF,得到$\frac{AD}{BE}$=$\frac{AE}{BF}$,代入即可,
②得出函数关系式后,可以发现点E自运动开始到停止运动所走的路线长度是函数的最大值的二倍,据此即可得解;
(3)根据条件可知△DCA′∽△A′BE,再根据三边之间的对应关系与x的取值范围求解,即可得出.
解答 解:(1)如图1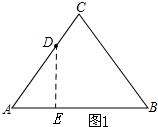
当DE⊥AB时,
在Rt△AED中,AD=6,∠A=60°,
AE=AD•cosA=6×cos60°=3,
∴当x=3时,DE⊥AB;
(2)①∵△ABC是等边三角形,
∴在△ABC中,∠A=60°,AB=AC=BC=9,
∴∠ADE+∠AED=120°;
又∵∠DEF=60°,
∴∠BEF+∠AED=120°,
∴∠ADE=∠BEF;
∴△ADE∽△BEF,
∴$\frac{AD}{BE}$=$\frac{AE}{BF}$,
$\frac{6}{9-x}$=$\frac{x}{y}$,∴y=-$\frac{1}{6}$x2+$\frac{3}{2}$x=-$\frac{1}{6}$(x-$\frac{9}{2}$)2+$\frac{27}{8}$,
当x=$\frac{9}{2}$时,y最大=$\frac{27}{8}$,
②由①知,y=$-\frac{1}{6}$x2+$\frac{3}{2}$x,
当x=0时,y=0,当x=9时,y=0,
即:点F运动到离点B最远处时,BF=$\frac{27}{8}$,此后再回到B点,
∴点F运动路线的总长为:$\frac{27}{8}×2$=$\frac{27}{4}$(cm);
(3)存在,
∵△ABC是等边三角形,∴AB=AC=BC=9cm,
∠A=∠B=∠C=60°,
如图2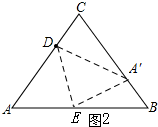
当点A的对称点A′落在线段BC上时,
DA′=DA=6,A′E=AE=x,∠DA′E=∠A=60°,
∴∠DA′C+∠EA′B=120°,
又∠CDA′+∠DA′C=120°,
∴∠CDA′=∠EA′B,
又∵∠B=∠C=60°,
∴△DCA′∽△A′BE,
∴$\frac{DA′}{A′E}=\frac{DC}{A′B}=\frac{CA′}{BE}$,
∴$\frac{6}{x}=\frac{3}{A′B}$,
解得:A′B=$\frac{x}{2}$,
∴$\frac{6}{x}=\frac{9-\frac{x}{2}}{9-x}$,
整理得:x2-30x+108=0,
解得:x1=$15+3\sqrt{13}$(舍),${x}_{2}=15-3\sqrt{13}$,
∴当x=$15-3\sqrt{13}$时,点A的对称点A′恰好落在线段BC上.
点评 本题主要考查了三角形相似的判定定理与性质定理,以及用二次函数求最值的问题,灵活运用相似三角形的知识是解题的关键,在第(2)问中要注意是要求点F运动路线的总长,注意总结.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:选择题
| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后, 便不能再涨,叫涨停;当跌了原价的10%后,便不能再跌,叫跌停.已知一支股票某天跌停,之后两天时间又张回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是( )
便不能再涨,叫涨停;当跌了原价的10%后,便不能再跌,叫跌停.已知一支股票某天跌停,之后两天时间又张回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是( )
A. 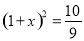 B.
B. 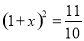 C.
C. 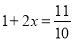 D.
D. 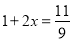
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 北京 | 上海 | 杭州 | 苏州 | 武汉 | 重庆 | 广州 | 福州 | 南宁 | 深圳 |
| 最高温度(℃) | 21 | 25 | 28 | 27 | 26 | 31 | 29 | 28 | 30 | 29 |
| A. | 27 | B. | 28 | C. | 29 | D. | 31 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com