
 ,x1•x2=
,x1•x2= ,
, <0,
<0, ,
, <0,
<0, >0,
>0, 有意义,
有意义, ,x1•x2=
,x1•x2= ,再假设△ABC能构成为直角三角形,则x1•x2<0,即
,再假设△ABC能构成为直角三角形,则x1•x2<0,即 <0,根据勾股定理可得出q2=-
<0,根据勾股定理可得出q2=- ,即pq=-1.
,即pq=-1. <0是解答此题的关键.
<0是解答此题的关键. 

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
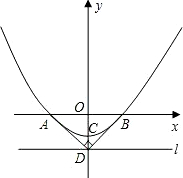 行于x轴的一条直线.
行于x轴的一条直线.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(43):2.7 最大面积是多少(解析版) 题型:解答题
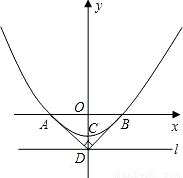
查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(47):34.4 二次函数的应用(解析版) 题型:解答题
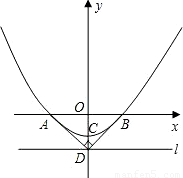
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(43):2.4 二次函数的应用(解析版) 题型:解答题
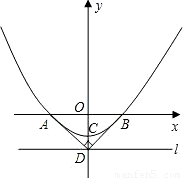
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com