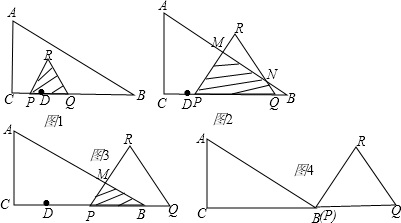
解:(1)△PQR的边长PQ=CQ-CP=(CD+DQ)-CP=(1+2t)-t=(t+1)cm;
∵当t为某值时,点R落在AB上,三角形RPQ是等边三角形,
∴QB=QR=QP=t+1,∠RQD=60°,
∴∠RQB=120°,∠QRB=30°,
∴△QRB为等腰三角形,
∵QB=CB-CP-PQ=6-t-(t+1)=5-2t,
∴5-2t=t+1,
解得:t=

s;
(2)分为四种情况:①当0≤t<

时,如图1:重叠部分是△RPQ,
∵△RPQ的边长为t+1,
∴高为

(t+1)cm,
∴y=

×(t+1)×

(t+1)=

(t+1)
2;
②当

≤t<

时,如图2:重叠部分为四边形MNQP,
∵∠B=30°,且△RPQ为等边三角形,
∴∠RPQ=∠R=60°,
∴∠PMN=90°,且PB=BC-CP=6-t,∠RNM=30°,
∴PM=

(6-t),
∴MR=PR-PM=(t+1)-

(6-t)=

(3t-4),
∴MN=MR•tan60°=

(3t-4),
∴y=

(t+1)
2-

(3t-4)
2
=-
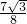
t
2+
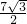
t-
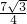
=-
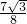
(t-2)
2+
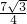
;
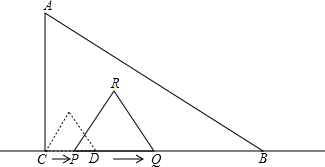
③当

≤t<6时,如图3:同理可得y=

(6-t)
2;
④当t≥6时,如图4:此时y=0.
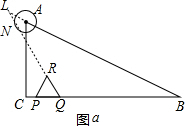
(3)(一)如图a,
⊙A与RQ所在的直线相切时,切点为N,N在QR的延长线上,AB与NQ交于L点,
AN=t,得到AL=2t,
QB=5-2t,得到BL=

(5-2t),
AB=4

=BL-AL=

(5-2t)-2t,
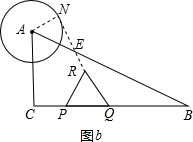
得到t=
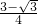
.
即t=
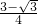
.
如图b,若NR交AB与E,
∵⊙A半径=AN=t,则AE=2t,QE=QB=5-2t,BE=

(5-2t),
AB=4

=BE+AE=

(5-2t)+2t,
∴t=
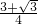
,
(二)如图c:
当⊙A与PQ所在的直线相切时,
∵AC⊥PQ所在的直线,
∴⊙A半径=AC=t=2

.
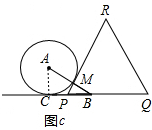
此时,若设AB与PR相交于M,
则AM=⊙A半径=2

,
∴BM=4

-2

=2

,
∴∠PMB=90°,
∴⊙A 也同时与PR相切.
(三)如图d:
⊙A与PR所在的直线相切时,切点为M,可知道点M在AB延长线上,
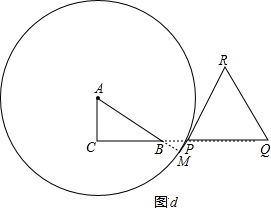
在Rt△PBM中,∠ABC=30°,有AM=t,BM=AM-AB=t-4

,斜边PB=CP-BC=t-6,
所以

PB=BM,有

(t-6)=t-4

,
得到t=4

+6;
综上所述,当⊙A与QR所在的直线相切时,t=
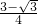
或t=
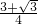
,;
当⊙A与PQ所在的直线相切时,t=2

;
当⊙A与PR所在的直线相切,t=2

或者t=4

+6.
分析:(1)根据题意,直接将△PQR的三边相加即可得出含t的表达式;易得△QRB为等腰三角形,可得到QB=QR=QP=t+1,又QB=CB-CP-PQ,两式联立即有5-2t=t+1,解之即可得出t.
(2)易得重叠部分为一个小等边三角形,依题意分别得出底边及其对应的高即可得出重叠部分的面积.
(3)结合题意,可知有三种情况,①以点A为圆心、tcm为半径的⊙A与PQ所在的直线相切,②⊙A与PQ所在的直线相切,③⊙A与RQ所在的直线相切;分别利用切线的性质以及勾股定理,即可得出各种情况对应的t值.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,最后一问属于开放性试题,主要考查的是切线性质的实际应用;本题是一道动态几何题,综合性较强,有一定的难度.

 解:(1)△PQR的边长PQ=CQ-CP=(CD+DQ)-CP=(1+2t)-t=(t+1)cm;
解:(1)△PQR的边长PQ=CQ-CP=(CD+DQ)-CP=(1+2t)-t=(t+1)cm; s;
s; 时,如图1:重叠部分是△RPQ,
时,如图1:重叠部分是△RPQ, (t+1)cm,
(t+1)cm, ×(t+1)×
×(t+1)× (t+1)=
(t+1)= (t+1)2;
(t+1)2; ≤t<
≤t< 时,如图2:重叠部分为四边形MNQP,
时,如图2:重叠部分为四边形MNQP, (6-t),
(6-t), (6-t)=
(6-t)= (3t-4),
(3t-4), (3t-4),
(3t-4), (t+1)2-
(t+1)2- (3t-4)2
(3t-4)2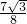 t2+
t2+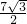 t-
t-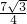
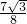 (t-2)2+
(t-2)2+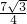 ;
; ≤t<6时,如图3:同理可得y=
≤t<6时,如图3:同理可得y= (6-t)2;
(6-t)2;
 (5-2t),
(5-2t), =BL-AL=
=BL-AL= (5-2t)-2t,
(5-2t)-2t,
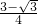 .
.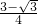 .
. (5-2t),
(5-2t), =BE+AE=
=BE+AE= (5-2t)+2t,
(5-2t)+2t,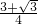 ,
, .
.
 ,
, -2
-2 =2
=2 ,
,
 ,斜边PB=CP-BC=t-6,
,斜边PB=CP-BC=t-6, PB=BM,有
PB=BM,有 (t-6)=t-4
(t-6)=t-4 ,
, +6;
+6;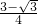 或t=
或t=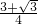 ,;
,; ;
; 或者t=4
或者t=4 +6.
+6.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案