
 重合,点A在x轴上,点B在y轴上OB=
重合,点A在x轴上,点B在y轴上OB=| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| OE |
| OB |
| OE | ||
|
| ||
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
2
| ||
| 9 |
2
| ||
| 9 |
2
| ||
| 3 |
| 3 |
|
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
| ||
| 4 |
| 9 |
| 4 |
| ||
| 4 |
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 4 |
| ||
| 4 |
| 9 |
| 4 |
| ||
| 4 |
| ||
| 3 |
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(
|
| ||
| 2 |
(
|
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
 
练习册系列答案
 天天向上一本好卷系列答案 天天向上一本好卷系列答案 小学生10分钟应用题系列答案 小学生10分钟应用题系列答案
相关习题
科目:初中数学 来源:不详 题型:解答题 已知二次函数的图象过(0,3),(3,0),且对称轴为直线x=1. (1)求这个二次函数的图象的解析式; (2)指出二次函数图象的顶点坐标; (3)利用草图分析,当函数值y>0时,x的取值范围是多少. 查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 如图,抛物线y=-
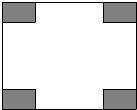
(1)求点A、B的坐标; (2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标; (3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式. 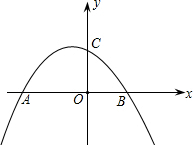 查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 抛物线y=mx2+(m-3)x-3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC. (1)求这条抛物线的解析式; (2)若点P(x1,b)与点Q(x2,b)在(1)中的抛物线上,且x1<x2,PQ=n. ①求4x12-2x2n+6n+3的值; ②将抛物线在PQ下方的部分沿PQ翻折,抛物线的其它部分保持不变,得到一个新图象.当这个新图象与x轴恰好只有两个公共点时,b的取值范围是______. 查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 已知如图,对称轴为直线x=4的抛物线y=ax2+2x与x轴相交于点B、O. (1)求抛物线的解析式. (2)连接AB,平移AB所在的直线,使其经过原点O,得到直线l.点P是l上一动点,当△PAB的周长最小时,求点P的坐标. (3)当△PAB的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似?若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O)  查看答案和解析>> 科目:初中数学 来源:不详 题型:解答题 某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.设每块绿化区的长边为xm,短边为ym,工程总造价为w元. (1)写出x的取值范围; (2)写出y与x的函数关系式; (3)写出w与x的函数关系式; (4)如果小区投资46.9万元,问能否完成工程任务?若能,请写出x为整数的所有工程方案;若不能,请说明理由.(参考数据:
 查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |