C
分析:假设梯形ABCD,此时作DE∥AB,则能使△CED成立的组合即可构成梯形,从而讨论:
①a=5为上底,b=10为下底,c、d为腰,②a=5为上底,b=15为下底,b、d为腰,③a=5为上底,b=20为下底,b、c为腰,④b=10为上底,c=15为下底,a、d为腰,⑤b=10为上底,d=20为下底,a、c为腰,⑥c=15为上底,d=20 为下底,a、b为腰,得出满足题意的组合即可得出答案.
解答:
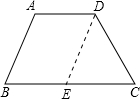
解:作DE∥AB,则DE=AB,
①当a=5为上底,b=10为下底,c、d为腰时,10-5=5,与15,20不能构成三角形,故不满足题意;
②当a=5为上底,b=15为下底,b、d为腰时,15-5=10,与10,20不能构成三角形,故不满足题意;
③当a=5为上底,b=20为下底,b、c为腰时,20-5=15,与10,15可以构成三角形,故满足题意;
④当b=10为上底,c=15为下底,a、d为腰时,15-10=5,与5,20不能构成三角形,故不满足题意;
⑤当b=10为上底,d=20为下底,a、c为腰时,20-10=10,与5,15不能构成三角形,故不满足题意;
⑥当c=15为上底,d=20 为下底,a、b为腰时,20-15=5,与5,10不能构成三角形,故不满足题意;
综上可得只有当a=5为上底,b=20为下底,b、c为腰时,满足题意,即以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)只能做一个.
故选C.
点评:此题考查了梯形及三角形的三边关系,难点在于分类讨论上底、下底的值,判断CDE是否可以构成三角形,要求我们掌握三角形的两边之和大于第三边,两边之差小于第三边.

 解:作DE∥AB,则DE=AB,
解:作DE∥AB,则DE=AB,

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案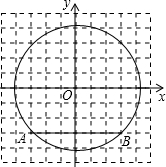 如图,以原点O为圆心作一个半径为3
如图,以原点O为圆心作一个半径为3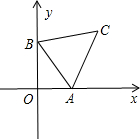 如图,直线y=-
如图,直线y=-
 如图一次函数y=-
如图一次函数y=-