
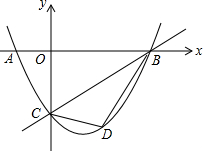
 ШчЭМЃЌжБЯпy=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпy=ax2+bx-$\sqrt{3}$ОЙ§ЕуAЁЂBЁЂCЃЌЧвЕуAзјБъЪЧЃЈ-1ЃЌ0ЃЉЃЌЕуDЪЧжБЯпBCЯТЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЎ
ШчЭМЃЌжБЯпy=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$гыxжсНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпy=ax2+bx-$\sqrt{3}$ОЙ§ЕуAЁЂBЁЂCЃЌЧвЕуAзјБъЪЧЃЈ-1ЃЌ0ЃЉЃЌЕуDЪЧжБЯпBCЯТЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЎЗжЮі ЃЈ1ЃЉИљОнздБфСПгыКЏЪ§жЕЕФЖдгІЙиЯЕЃЌПЩЕУBЕузјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЦНаагкyжсжБЯпЩЯСНЕуМфЕФОрРыЪЧНЯДѓЕФзнзјБъМфНЯаЁЕФзнзјБъЃЌПЩЕУDFЕФГЄЃЌИљОнУцЛ§ЕФКЭВюЃЌПЩЕУЖўДЮКЏЪ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЃЌПЩЕУД№АИЃЛ
ЃЈ3ЃЉИљОнЙДЙЩЖЈРэЃЌПЩЕУЙигкnЕФЗНГЬЃЌИљОнНтЗНГЬЃЌПЩЕУnЕФжЕЃЌдйИљОнЙДЙЩЖЈРэЃЌПЩЕУД№АИЃЎ
НтД№ НтЃКЃЈ1ЃЉгЩy=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$ЃЌЕУy=0ЪБЃЌx=3ЃЌBЕузјБъЮЊЃЈ3ЃЌ0ЃЉЃЌ
НЋAЁЂBЕузјБъДњШыКЏЪ§НтЮіЪНЃЌЕУ
$\left\{\begin{array}{l}{a-b-\sqrt{3}=0}\\{9a+3b-\sqrt{3}=0}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$ЃЌ
y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$ЃЛ
ЃЈ2ЃЉШчЭМ1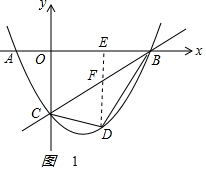 ЃЌЙ§ЕуDзїDEЁЭxжсгкЕуEНЛBCгкFЕуЃЌ
ЃЌЙ§ЕуDзїDEЁЭxжсгкЕуEНЛBCгкFЕуЃЌ
ЩшDЕуЕФзјБъЮЊЃЈmЃЌ$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$ЃЉЕуFЕФзјБъЮЊЃЈmЃЌ$\frac{\sqrt{3}}{3}$m-$\sqrt{3}$ЃЉ
DF=ЃЈ$\frac{\sqrt{3}}{3}$m-$\sqrt{3}$ЃЉ-ЃЈ$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$ЃЉ=-$\frac{\sqrt{3}}{3}$m2+$\sqrt{3}$mЃЌ
SЫФБпаЮABDC=SЁїDFB+SЁїDFC+SЁїABC
=$\frac{1}{2}$DF•OB+$\frac{1}{2}$ЁС4ЁС$\sqrt{3}$
=$\frac{1}{2}$ЃЈ-$\frac{\sqrt{3}}{3}$m2+$\sqrt{3}$mЃЉЁС3+2$\sqrt{3}$
=-$\frac{\sqrt{3}}{2}$ЃЈm-$\frac{3}{2}$ЃЉ2+$\frac{25\sqrt{3}}{8}$ЃЈ0ЃМmЃМ3ЃЉЃЌ
ЁрЕБm=$\frac{3}{2}$ЪБЃЌЫФБпаЮABDCЕФУцЛ§ШЁЕУзюДѓжЕ$\frac{25\sqrt{3}}{8}$ЃЌДЫЪБЕуDЕФзјБъЮЊЃЈ$\frac{3}{2}$ЃЌ-$\frac{5\sqrt{3}}{4}$ЃЉЃЛ
ЃЈ3ЃЉy=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$=$\frac{\sqrt{3}}{3}$ЃЈx-1ЃЉ2-$\frac{4\sqrt{3}}{3}$ЃЌ
ЖдГЦжсгкxжсЕФНЛЕуEЮЊЃЈ1ЃЌ0ЃЉЃЌ
CEЕФНтЮіЪНЮЊy=$\sqrt{3}$x-$\sqrt{3}$ЃЌ
ЩшPЕузјБъЮЊЃЈnЃЌ$\sqrt{3}$n-$\sqrt{3}$ЃЉЃЌPдкCEЕФЩфЯпЩЯЃЌЁрЁЯPABЃМ90ЁуЃЌ
AP2=ЃЈn+1ЃЉ2+ЃЈ$\sqrt{3}n-\sqrt{3}$ЃЉ2ЃЌPB2=ЃЈn-3ЃЉ2+ЃЈ$\sqrt{3}$n-$\sqrt{3}$ЃЉ2
ЂйЕБЁЯAPB=90ЁуЪБЃЌAP2+PB2=AB2ЃЌ
МДЃЈn+1ЃЉ2+ЃЈ$\sqrt{3}$n-$\sqrt{3}$ЃЉ2+ЃЈn-3ЃЉ2+ЃЈ$\sqrt{3}$n-$\sqrt{3}$ЃЉ2=42ЃЌ
ЛЏМђЃЌЕУ8n2-16n=0ЃЌ
НтЕУn1=0ЃЌn2=2ЃЌ
ЕБn=0ЪБЃЌAP=$\sqrt{ЃЈ0+1ЃЉ^{2}+ЃЈ-\sqrt{3}ЃЉ^{2}}$=2ЃЌ
ЕБn=2ЪБЃЌAP=$\sqrt{ЃЈ2+1ЃЉ^{2}+ЃЈ2\sqrt{3}-\sqrt{3}ЃЉ^{2}}$=2$\sqrt{3}$ЃЛ
ЂкЕБЁЯABP=90ЁуЪБЃЌBPЁЭABгкBЃЌЕУ
n=3ЃЌ
AP=$\sqrt{ЃЈ3+1ЃЉ^{2}+ЃЈ3\sqrt{3}-\sqrt{3}ЃЉ^{2}}$=2$\sqrt{7}$ЃЌ
злЩЯЫљЪіЃКAPЕФГЄЮЊ2ЃЌ2$\sqrt{3}$ЃЌ2$\sqrt{7}$ЃЎ
ЕуЦР БОЬтПМВщСЫЖўДЮКЏЪ§злКЯЬтЃЌНтЃЈ1ЃЉЕФЙиМќЪЧД§ЖЈЯЕЪ§ЗЈЃЌНтЃЈ2ЃЉЕФЙиМќЪЧРћгУУцЛ§ЕФКмВюЕУГіЖўДЮКЏЪ§ЃЌгжРћгУСЫЖўДЮКЏЪ§ЕФаджЪЃЛНтЃЈ3ЃЉЕФЙиМќЪЧЙДЙЩЖЈРэЕУГіЙигкnЕФЗНГЬЃЌвЊЗжРрЬжТлЃЌвдЗРвХТЉЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
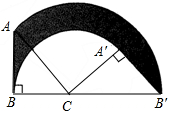 ШчЭМЃЌЕШбќRtЁїABCжаЃЌЁЯB=90ЁуЃЌAB=1ЃЌНЋRtЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЌЕУЕНRtЁїAЁфBЁфCЃЌЧвBЁЂCЁЂBЁфШ§ЕуЙВЯпЃЌдђБпABЩЈЙ§ЕФУцЛ§ЃЈЭМжавѕгАВПЗжЃЉЪЧ$\frac{3}{8}Іа$ЃЎ
ШчЭМЃЌЕШбќRtЁїABCжаЃЌЁЯB=90ЁуЃЌAB=1ЃЌНЋRtЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЌЕУЕНRtЁїAЁфBЁфCЃЌЧвBЁЂCЁЂBЁфШ§ЕуЙВЯпЃЌдђБпABЩЈЙ§ЕФУцЛ§ЃЈЭМжавѕгАВПЗжЃЉЪЧ$\frac{3}{8}Іа$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ |  | BЃЎ |  | CЃЎ |  | DЃЎ |  |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com