在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
(1)已知a=40,c=41,求b;
(2)已知a:b=3:4,c=15,求b;
(3)已知c=50,a=30,CD⊥AB于D,求CD.
解:(1)根据勾股定理得,
b=

=
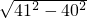
=9;
(2)∵a:b=3:4,
∴a=

b,
由勾股定理得,
a
2+b
2=c
2,
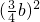
+b
2=15
2,
解得b=12;
(3)如图,
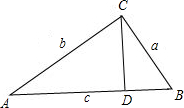
根据勾股定理得,
b=

=

=40,
S
△ABC=

ab=

c×CD,

×40×30=

×50×CD,
解得CD=24.
分析:(1)直接运用勾股定理解答即可;
(2)把a用b表示,再利用勾股定理解答即可;
(3)先利用勾股定理求得b,再利用三角形的面积解答即可.
点评:此题考查勾股定理及三角形的面积计算方法.
