
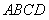 的顶点
的顶点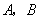 的坐标分别为
的坐标分别为 ,顶点
,顶点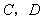 在第一象限.点P从点A出发,沿正方形按逆时针方向匀速运动,同时,点Q从点
在第一象限.点P从点A出发,沿正方形按逆时针方向匀速运动,同时,点Q从点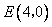 出发,沿x轴正方向以相同速度运动.当P点到达点C时,
出发,沿x轴正方向以相同速度运动.当P点到达点C时,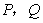 两点同时停止运动,设运动的时间为t秒.
两点同时停止运动,设运动的时间为t秒.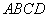 的边长.
的边长.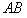 上运动时,
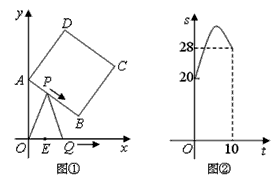
上运动时,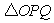 的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分(如图②所示),求
的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分(如图②所示),求 两点的运动速度.
两点的运动速度.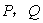 保持(2)中的速度不变,则点P沿着AB边运动时,
保持(2)中的速度不变,则点P沿着AB边运动时,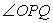 的大小随着时间t的增大而增大;沿着
的大小随着时间t的增大而增大;沿着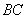 边运动时,
边运动时,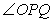 的大小随着时间t的增大而减小.当点P沿着这两边运动时,使
的大小随着时间t的增大而减小.当点P沿着这两边运动时,使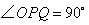 的点P有_____个.
的点P有_____个. 的顶点坐标是
的顶点坐标是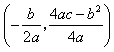 .)
.) 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com