
分析 ①消去小括号后,再根据有理数的加减进行计算即可得出结论;
②根据乘法分配律将算式算式展开,再进行计算即可得出结论;
③变小数为分数,变除为乘,在进行计算即可得出结论;
④根据混合运算的运算顺序结合有理数的乘方,即可得出算式的结果.
解答 解:①原式=-3-4-11+19=1;
②原式=$\frac{2}{3}$×(-24)-$\frac{1}{4}$×(-24)-$\frac{3}{8}$×(-24)=-16+6+9=-1;
③原式=-$\frac{7}{2}$×$\frac{8}{7}$×(-$\frac{8}{7}$)×$\frac{3}{64}$=$\frac{3}{14}$;
④原式=-1-$\frac{1}{2}$×$\frac{1}{3}$×[2-9]=-1+$\frac{7}{6}$=$\frac{1}{6}$.
点评 本题考查了有理数的混合运算、有理数的乘方以及绝对值,熟练掌握有理数混合运算的运算顺序是解题的关键.


科目:初中数学 来源: 题型:解答题
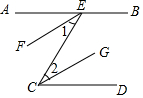 填写证明的理由.
填写证明的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
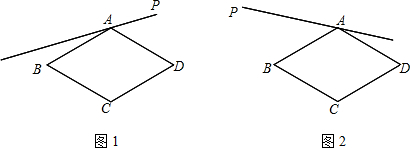
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
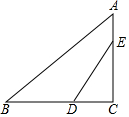 如图,在Rt△ABC中,∠C=90°,AB=5,AC=3,点D、E分别是边BC、AC上的点,且∠EDC=∠A,将△ABC沿DE翻折,若点C恰好落在边AB上,则 DE的长为$\frac{125}{48}$.
如图,在Rt△ABC中,∠C=90°,AB=5,AC=3,点D、E分别是边BC、AC上的点,且∠EDC=∠A,将△ABC沿DE翻折,若点C恰好落在边AB上,则 DE的长为$\frac{125}{48}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com