
����Ŀ����ͼ1���ڡ�ABC�У����A����B����C�ĶԱ߷ֱ�Ϊa��b��c������A��AD��BC������ΪD������sin��C= ![]() ����
����
S��ABC= ![]() BC��AD=
BC��AD= ![]() ��BC��ACsin��C=
��BC��ACsin��C= ![]() absin��C��
absin��C��
��S��ABC= ![]() absin��C
absin��C
ͬ��S��ABC= ![]() bcsin��A
bcsin��A
S��ABC= ![]() acsin��B
acsin��B
ͨ�����������Եõ���һ�����������α߽ǹ�ϵ�Ķ��������Ҷ�����
��ͼ2���ڡ�ABC�У�����A����B����C�ĶԱ߷ֱ�Ϊa��b��c����
a2=b2+c2��2bccos��A
b2=a2+c2��2accos��B
c2=a2+b2��2abcos��C
������������������ʽ�����Ҷ���������⣺
��1����ͼ3���ڡ�DEF�У���F=60�㣬��D����E�ĶԱ߷ֱ���3��8����S��DEF��DE2 �� 
�⣺S��DEF= ![]() EF��DFsin��F=��
EF��DFsin��F=��
DE2=EF2+DF2��2EF��DFcos��F= ��
��2����ͼ4���ڡ�ABC�У���֪AC��BC����C=60�㣬��ABC'����BCA'����ACB'�ֱ�����AB��BC��ACΪ�߳��ĵȱ������Σ����ABC����ABC'����BCA'����ACB'������ֱ�ΪS1��S2��S3��S4 �� ��֤��S1+S2=S3+S4 �� 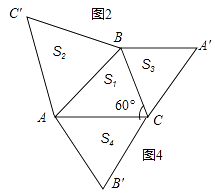
���𰸡�
��1��6 ![]() ��49
��49
��2��
֤��������1���ߡ�ACB=60�㣬
��AB2=AC2+BC2��2ACBCcos60��=AC2+BC2��ACBC��
����ͬʱ���� ![]() sin60��ã�
sin60��ã� ![]() AB2sin60��=
AB2sin60��= ![]() AC2sin60��+
AC2sin60��+ ![]() BC2sin60�㩁
BC2sin60�㩁 ![]() ACBCsin60�㣬
ACBCsin60�㣬
�ߡ�ABC'����BCA'����ACB'�ǵȱ������Σ�
��S1= ![]() ACBCsin60�㣬S2=
ACBCsin60�㣬S2= ![]() AB2sin60�㣬S3=
AB2sin60�㣬S3= ![]() BC2sin60�㣬S4=
BC2sin60�㣬S4= ![]() AC2sin60�㣬
AC2sin60�㣬
��S2=S4+S3��S1��
��S1+S2=S3+S4��
����2�����A����B����C�ĶԱ߷ֱ�Ϊa��b��c��
��S1= ![]() absin��C=
absin��C= ![]() absin60��=
absin60��= ![]() ab
ab
�ߡ�ABC'����BCA'����ACB'�ǵȱ������Σ�
��S2= ![]() ccsin60��=
ccsin60��= ![]() c2��S3=
c2��S3= ![]() aasin60��=
aasin60��= ![]() a2��S4=
a2��S4= ![]() bbsin60��=
bbsin60��= ![]() b2��
b2��
��S1+S2= ![]() ��ab+c2����S3+S4=
��ab+c2����S3+S4= ![]() ��a2+b2����
��a2+b2����
��c2=a2+b2��2abcos��C=a2+b2��2abcos60�㣬
��a2+b
��S1+S2=S3+S4
���������⣺��1���ڡ�DEF�У���F=60�㣬��D����E�ĶԱ߷ֱ���3��8��
��EF=3��DF=8��
��S��DEF= ![]() EF��DFsin��F=
EF��DFsin��F= ![]() ��3��8��sin60��=6
��3��8��sin60��=6 ![]() ��
��
DE2=EF2+DF2��2EF��DFcos��F=32+82��2��3��8��cos60��=49��
���Դ��ǣ�6 ![]() ��49��
��49��
�����㾫��������ͬ�����Ǻ����Ĺ�ϵ��������ƽ�����̣��ǽ����ĸ�������Ҫ֪����������Ǻ���֮��Ĺ�ϵ��ƽ����ϵ��sin2A+cos2A=1����������ϵ��tanAtan(90�㡪A)=1�������й�ϵ��tanA=sinA/cosA ����


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AC��BD����E��F��G��H�ֱ���AB��BC��CD��DA���е㣬�������Ӹ����е�õ��ı���EFGH����֤���ı���EFGH�Ǿ��Σ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���BD�ϵ����㣬��BF=ED����֤��AE��CF�� 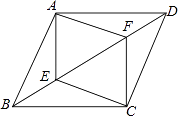
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ���һ�γ���֪ʶ����������10�֣�ѧ���÷־�Ϊ�������ɼ��ﵽ6�ּ�6������Ϊ�ϸﵽ9�ֻ�10��Ϊ���㣬��ξ����У��ס�������ѧ���ɼ��ֲ�������ͳ��ͼ�ͳɼ�ͳ�Ʒ�������ͼ��ʾ��
��1��������гɼ�ͳ�Ʒ�������a��b��ֵ��
��� | ƽ���� | ��λ�� | ���� | �ϸ��� | ������ |
���� | 6.8 | a | 3.76 | 90% | 30% |
���� | b | 7.5 | 1.96 | 80% | 20% |
��2��СӢͬѧ˵������ξ����ҵ���7�֣�������С����������������ƫ�ϣ����۲���������жϣ�СӢ�Ǽס����ĸ����ѧ����
��3������ͬѧ˵������ĺϸ��ʡ������ʾ��������飬����������ijɼ��������飮������ͬѧ��ͬ�����ͬѧ��˵������Ϊ������ijɼ�Ҫ���ڼ��飮����д������֧������ͬѧ�۵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ǿ��ѧ�������ʣ�ijУʳ��ÿ�춼Ϊѧ���ṩһ��������ˮ����ѧУ����ʦΪ���˽�ѧ��ϲ��������ˮ���������˳������飬�����Ϊ�������ͣ�Aϲ����ƻ����ѧ����Bϲ���Խ��ӵ�ѧ����C��ϲ�������ѧ����D��ϲ�����㽶��ѧ����Eϲ�������ϵ�ѧ�����������������Ƴ�ͼ1��ͼ2 ��ͳ��ͼ�����������������ͼ���ṩ�����ݽ���������⣺ 
��1����˴γ���ѧ��������
��2����ͼ2��������������ͼ1�е�x��
��3������5��ѧ��������A����3����B����2����������ѡ2��ѧ���μ����ܲ��ԣ���������ѧ��Ϊͬһ���͵ĸ��ʣ����б�������״ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������
��1����22+����2017��0��2sin60��+|1�� ![]() |��
|��
��2��a��3��2a��+2��a+1����a��1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4����P��AB���ϵ�һ�����㣬����CP������P��PC�Ĵ��߽�AD�ڵ�E���� PEΪ����������PEFG������G���߶�PC�ϣ��Խ���EG��PF�ཻ�ڵ�O�� 
��1����AP=1����AE=��
��2������֤����Oһ���ڡ�APE�����Բ�ϣ� �ڵ���P�ӵ�A�˶�����Bʱ����OҲ��֮�˶������O������·������
��3���ڵ�P�ӵ�A����B���˶������У���APE�����Բ��Բ��Ҳ��֮�˶������Բ�ĵ�AB�ߵľ�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��0������{an}����an+1=|p��an|+2an+p��n��N*��
��1����a1=��1��p=1�� ����a4��ֵ��
��������{an}��ǰn���Sn��
��2��������{an}�д�������ar �� as �� at��r��s��t��N*��r��s��t�����γɵȲ����У��� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�EΪDC���ϵĵ㣬����BE������BCE�Ƶ�C˳ʱ�뷽����ת90��õ���DCF������EF������BEC=60�㣬���EFD�Ķ���Ϊ�� �� 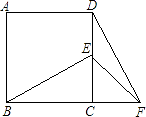
A.10��
B.15��
C.20��
D.25��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com