Question

在教材中，我们通过数格子的方法发现了直角三角形的三边关系，利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性。

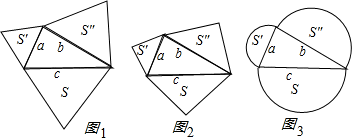
问题1：以直角三角形的三边为边向形外作等边三角形，探究S₁+S₂与S₃的关系（如图1）。
问题2：以直角三角形的三边为斜边向形外作等腰直角三角形，探究S'+S''与S的关系（如图2）。
问题3：以直角三角形的三边为直径向形外作半圆，探究S₁+S₂与S₃的关系（如图3）。

Answer 1

解：探究1：由等边三角形的性质知：
S₁=a²，S₂=b²，S₃=c²，
则S₁+S₂=（a²+b²），
因为a²+b²=c²，所以S₁+S₂=S_3。
探究2：由等腰直角三角形的性质知：
S'=a²，S''=b²，S=c²，
则S'+S''=（a²+b²），
因为a²+b²=c²，所以S'+S''=S。
探究3：由圆的面积计算公式知：
S₁=πa²，S₂=πb²，S₃=πc²，
则S₁+S₂=π（a²+b²），
因此a²+b²=c²，所以S₁+S₂=S₃。