Question

【题目】如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M．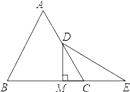

（1）求∠E的度数．
（2）求证：M是BE的中点．

Answer 1

【答案】
（1）解：∵三角形ABC是等边△ABC，

∴∠ACB=∠ABC=60°，

又∵CE=CD，

∴∠E=∠CDE，

又∵∠ACB=∠E+∠CDE，

∴∠E= ∠ACB=30°；

（2）证明：连接BD，

∵等边△ABC中，D是AC的中点，

∴∠DBC= ∠ABC= ×60°=30°

由（1）知∠E=30°

∴∠DBC=∠E=30°

∴DB=DE

又∵DM⊥BC

∴M是BE的中点．

【解析】（1）根据等边三角形的性质得出∠ACB的度数，由CE=CD得出∠E=∠CDE，再根据三角形的一个外角等于和它不相邻的两内角之和，求出∠E的度数。
（2）抓住已知条件等边△ABC中，D是AC的中点，由等腰三角形的三线合一的性质，可知应连接BD，得出BD平分∠ABC，求出∠DBC的度数，继而证得DB=DE，再根据等腰三角形的性质即可证得结论。
【考点精析】关于本题考查的等边三角形的性质，需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案．