
如图,抛物线F: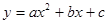 的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′:
的顶点为P,抛物线:与y轴交于点A,与直线OP交于点B.过点P作PD⊥x轴于点D,平移抛物线F使其经过点A、D得到抛物线F′: ,抛物线F′与x轴的另一个交点为C.
,抛物线F′与x轴的另一个交点为C.

⑴当a = 1,b=-2,c = 3时,求点C的坐标(直接写出答案);
⑵若a、b、c满足了
①求b:b′的值;
②探究四边形OABC的形状,并说明理由.
解:(1) C(3,0);
(2)①抛物线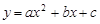 ,令
,令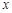 =0,则
=0,则 =
= ,
,
∴A点坐标(0,c).
∵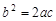 ,∴
,∴  ,
,
∴点P的坐标为( ).
).
∵PD⊥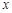 轴于D,∴点D的坐标为(
轴于D,∴点D的坐标为(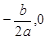 ).
).
根据题意,得a=a′,c= c′,∴抛物线F′的解析式为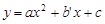 .
.
又∵抛物线F′经过点D(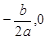 ),∴
),∴ .
.
∴ .
.
又∵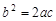 ,∴
,∴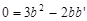 .
.
∴b:b′= .
.
②由①得,抛物线F′为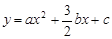 .
.
令y=0,则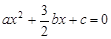 .
.
∴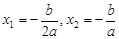 .
.
∵点D的横坐标为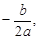 ∴点C的坐标为(
∴点C的坐标为( ).
).
设直线OP的解析式为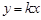 .
.
∵点P的坐标为( ),
),
∴ ,∴
,∴ ,∴
,∴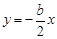 .
.
∵点B是抛物线F与直线OP的交点,∴ .
.
∴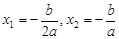 .
.
∵点P的横坐标为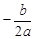 ,∴点B的横坐标为
,∴点B的横坐标为 .
.
把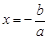 代入
代入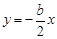 ,得
,得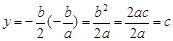 .
.
∴点B的坐标为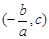 .
.
∴BC∥OA,AB∥OC.(或BC∥OA,BC =OA),
∴四边形OABC是平行四边形.
又∵∠AOC=90°,∴四边形OABC是矩形.
【解析】(1)先求出抛物线解析式,再根据平移的特征即可得到点C的坐标;
(2)①根据抛物线顶点坐标的表达式及抛物线与坐标轴的交点坐标的特征即可得到结果;
②根据抛物线与坐标轴的交点坐标及抛物线与直线OP的交点坐标的特征即可得到结果;


科目:初中数学 来源: 题型:
| 6 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 2 |
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
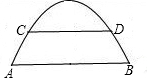 如图是抛物线拱桥,已知水位在AB位置时,水面宽4
如图是抛物线拱桥,已知水位在AB位置时,水面宽4| 6 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:《第27章 二次函数》2009年单元检测试卷(1)(解析版) 题型:解答题
 ,水位上升3m,达到警戒线CD,这时水面宽
,水位上升3m,达到警戒线CD,这时水面宽 .若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?
.若洪水到来时,水位以每小时0.25m的速度上升,求水过警戒线后几小时淹到拱桥顶?
查看答案和解析>>
科目:初中数学 来源:2001年青海省中考数学试卷(解析版) 题型:解答题
 米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
米,旗杆AB高为3米,C点的垂直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com