
一个圆锥的轴截面是等边三角形,它的高是 .
.
(1)求圆锥的侧面积和全面积;
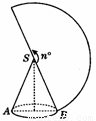
(2)画出圆锥的侧面展开图.
(1)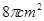 ,
,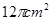 ;(2)如图所示:
;(2)如图所示:
【解析】
试题分析:(1)先根据等边三角形的性质求得母线及底面半径的长,再根据圆锥的侧面积和全面积公式即可求的结果;
(2)先根据扇形的面积公式求得扇形的圆心角,即可画出图形.
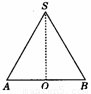
(1)如图为圆锥的轴截面,SA、SB为母线,SO为高,AB为底面圆的直径,所以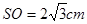
在Rt△SOB中,SB=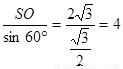 ,OB=SB·cos60°=4×
,OB=SB·cos60°=4×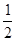 =2,
=2,
∴S侧=2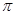 ·OB·
·OB·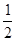 ·SB=2
·SB=2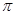 ×2×
×2×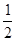 ×4=8
×4=8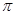
S全=S侧+S底=8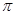 +
+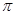 ·OB2=4
·OB2=4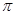 +8
+8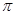 =12
=12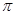 (cm2).
(cm2).
(2)设圆锥侧面展开图的圆心角为n°,由题意得
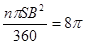 ,即
,即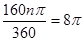 ,解得n=180,
,解得n=180,
所以圆锥的侧面展开图如图所示:

考点:等边三角形的性质,三角函数,扇形的面积公式
点评:作图能力是初中数学学习中一个极为基础的能力,是中考的热点,一般以作图题形式出现,难度不大,需熟练掌握.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2006-2007学年北京市西城区九年级(上)期末数学试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:期末题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com