
【题目】如图,B、C、D在同一直线上,△ABC和△DCE都是等边三角形,且在直线BD的同侧,BE交AD于F,BE交AC于M,AD交CE于N.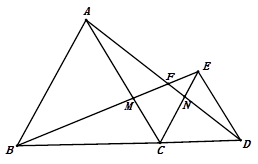
(1)求证:AD=BE;
(2)求证:△ABF∽△ADB。
【答案】
(1)
证明: ∵△ABC和△DCE都是等边三角形
∴BC=AC,CE=CD,![]() ACB=
ACB=![]() EDC=60°
EDC=60°
∴![]() ACB+
ACB+![]() ACE=
ACE=![]() EDC+
EDC+![]() ACE,即:
ACE,即:![]() BCE=
BCE=![]() ACD
ACD
在△BCE与△ACD 中,
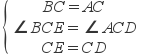
∴△BCE≌△ACD (SAS)
∴ AD=BE
(2)
证明:由(1)知:△BCE≌△ACD
∴ ∠CBE=∠CAD
又∵∠BMC=∠AMF
∴ ∠AFB=∠ACB=60°=∠ABC
又∵∠ABM=∠FBA
∴ △ABF∽△ADB
【解析】本题考查的是等边三角形的判定与性质、全等三角形的判定与性质及相似三角形的判定与性质,熟知全等三角形、相似三角形的判定定理,准确找出合适的全等三角形,再充分利用性质是解答此题的关键.


科目:初中数学 来源: 题型:
【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)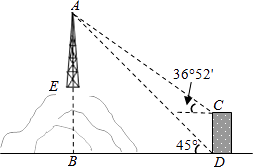
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查.整理样本数据,得到下列图表: 
(1)理解划线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由;
(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图; 
(3)该校数学兴趣小组结合调查获取信息,向学校提出了一些建议,如:骑车上学的学生约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8). 绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
(1)E类学生有人,补全条形统计图;
(2)D类学生人数占被调查总人数的%;
(3)从该班做义工时间在0≤t≤4的学生中任选2人,求这2人做义工时间都在2<t≤4中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3 , 等腰Rt△ABC的三个顶点A,B,C分别在l1 , l2 , l3上,∠ ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则AB:BD的值为( ) 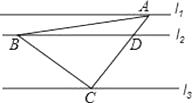
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+3x与x轴的正半轴交于点A,点B在抛物线上,且横坐标为2,作BC⊥x轴于点C,⊙B经过原点O,点E为⊙B上一动点,点F在AE上. 
(1)求点A的坐标;
(2)如图1,连结OE,当AF:FE=1:2时,求证:△ACF∽△AOE;
(3)如图2,当点F是AE的中点时,求CF的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com