
 的值总大于0.
的值总大于0.科目:初中数学 来源: 题型:
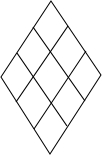 北京101中学的学生为迎接2008年奥运会,美化校园,在周长为12m,夹角为60°的菱形花坛里栽十株花.试证明:不论如何安排,至少有两株花的距离小于
北京101中学的学生为迎接2008年奥运会,美化校园,在周长为12m,夹角为60°的菱形花坛里栽十株花.试证明:不论如何安排,至少有两株花的距离小于| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com