
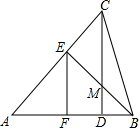
 在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.
在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.分析 (1)如图作EN⊥CD于N,先证明EN平分∠CEM,再证明∠ECM=∠EMC即可.
(2)先证明四边形EFDN是矩形,根据EF=DN=DM+MN,MN=$\frac{DC-DM}{2}$即可证明.
解答 证明:(1)如图,作EN⊥CD于N.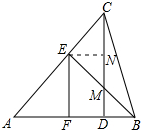 ∵EA=EB,
∵EA=EB,
∴∠A=∠EBA,
∵EN⊥CD,CD⊥AB,
∴EN∥AB,
∴∠CEN=∠A,∠NEM=∠EBA,
∴∠CEN=∠NEM,
∵∠ECN+∠CEN=90°,∠EMN+∠MEN=90°,
∴∠ECM=∠EMC,
∴EM=EC.
(2)结论:EF=$\frac{DM+CD}{2}$,
理由;∵EF平分∠AEB,EA=EB,
∴EF⊥AB,
∵∠EFD=∠FDN=∠END=90°,
∴四边形EFDN是矩形,
∴EF=DN,
∵EC=EM,EN⊥CM,
∴CN=NM,
∴EF=DM+MN=DM+$\frac{CD-DM}{2}$=$\frac{DM+CD}{2}$.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质和判定、矩形的判定等知识,解题的关键是添加辅助线,掌握利用等角的余角相等证明角相等,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
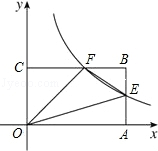 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
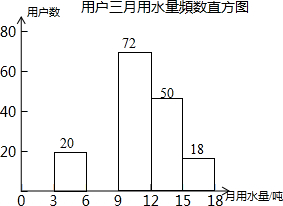 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用水量h(吨) | 频数 | 频率 |
| h≤3 | 0 | 0 |
| 3<h≤6 | 20 | 0.10 |
| 6<h≤9 | m | 0.20 |
| 9<h≤12 | 72 | 0.36 |
| 12<h≤15 | 50 | n |
| 15<h≤18 | 18 | 0.09 |
| 18<h | 0 | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{2}=1}\\{3x+6y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{3x+2y=7}\\{xy=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+y=1}\\{x+z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{5}{x}+\frac{y}{3}=\frac{1}{2}}\\{x+2y=3}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com