
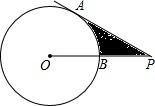
 如图,PA切⊙O于A,OP交⊙O于B,BP=2,AP=2
如图,PA切⊙O于A,OP交⊙O于B,BP=2,AP=2 cm,求图中阴影部分的周长和面积(结果保留π).
cm,求图中阴影部分的周长和面积(结果保留π).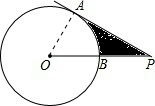 解:连接OA,由AP为圆O的切线,得到OA⊥AP,
解:连接OA,由AP为圆O的切线,得到OA⊥AP, cm,
cm, OP,
OP, 的长为
的长为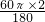 =
= ,S扇形AOB=
,S扇形AOB= =
= ,
, +2
+2 +2(cm),面积为S△AOP-S扇形AOB=
+2(cm),面积为S△AOP-S扇形AOB= ×2×2
×2×2 -
- =2
=2 -
- (cm2).
(cm2).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com