
如图1,在平面直角坐标系中,有一矩形ABCD,其三个顶点的坐标分别为A(2,0)、B(8,0)、C(8,3).将直线l:y=-3x-3以每秒3个单位的速度向右运动,设运动时间为t秒.


(1)当t=_________时,直线l经过点A.(直接填写答案)
(2)设直线l扫过矩形ABCD的面积为S,试求S>0时S与t的函数关系式.
(3)在第一象限有一半径为3、且与两坐标轴恰好都相切的⊙M,在直线l出发的同时,⊙M以每秒2个单位的速度向右运动,如图2所示,则当t为何值时,直线l与⊙M相切?
(1)1;
(2)当1<t≤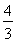 时,S=
时,S=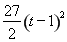 ;
;
当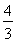 <t≤3时,S=9t-
<t≤3时,S=9t-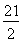 ;
;
当3<t≤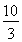 时,S=-
时,S=- (3t-10)2+18;
(3t-10)2+18;
当t>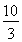 时,S=18;
时,S=18;
(3)t=5-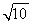 或t=5+
或t=5+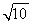 .
.
【解析】
试题分析:(1)y=-3x-3与x轴交点坐标是(-1,0),直线l经过点A(2,0),故向右平移3个单位长度,直线l:y=-3x-3以每秒3个单位的速度向右运动,所以t=1;
(2)求出直线l:y=﹣3x+9t﹣3,再分情况讨论;
(3)分两种情况讨论,借助三角形相似即可.
试题解析:(1)y=-3x-3与x轴交点坐标是(-1,0),直线l经过点A(2,0),故向右平移3个单位长度,直线l:y=-3x-3以每秒3个单位的速度向右运动,所以t=1;
(2)由题意,可知矩形ABCD顶点D的坐标为(2,3).
由一次函数的性质可知,当t由小到大变化时,直线l:y=﹣3(x﹣3t)-3=﹣3x+9t﹣3向右平移,依次扫过矩形ABCD的不同部分.
可得当直线经过A(2,0)时,t=1;当直线经过D(2,3)时,t=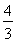 ;当直线经过B(8,0)时,t=3;当直线经过C(8,3)时,t=
;当直线经过B(8,0)时,t=3;当直线经过C(8,3)时,t=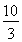 .
.
①当1<t≤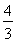 时, 如图所示.
时, 如图所示.
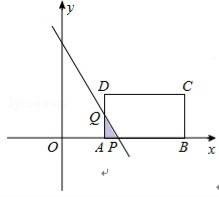
设直线l:y=-3x+9t﹣3与x轴交于点P,与AD交于点Q.
令y=0,可得x=3t﹣1,∴AP=3t﹣3;
令x=2,可得y=9t﹣9,∴AQ=9t﹣9.
∴S=S△APQ=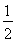 AP•AQ=
AP•AQ=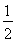 (3t﹣3)( 9t﹣9)=
(3t﹣3)( 9t﹣9)=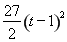 ;
;
②当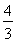 <t≤3时,如图所示.
<t≤3时,如图所示.
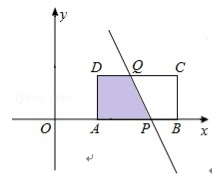
设直线l:y=-3x+9t﹣3与x轴交于点P,与CD交于点Q.
令y=0,可得x=3t﹣1,∴AP=3t﹣3;
令y=3,可得x=3t﹣2,∴DQ=3t﹣4.
S=S梯形APQD=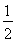 (DQ+AP)•AD=9t-
(DQ+AP)•AD=9t-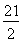 ;
;
③当3<t≤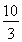 时,如图所示.
时,如图所示.
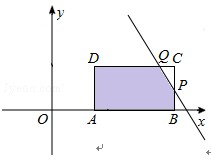
设直线l:y=-3x+9t﹣3与BC交于点P,与CD交于点Q.
令x=8,可得y=9t﹣27,∴BP=9t﹣27,CP=30﹣9t;
令y=3,可得x= 3t﹣2,∴DQ= 3t﹣4,CQ=10﹣3t.
S=S矩形ABCD﹣S△PQC=18﹣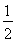 CP•CQ=-
CP•CQ=- (3t-10)2+18;
(3t-10)2+18;
④当t>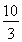 时,S=S矩形ABCD=18.
时,S=S矩形ABCD=18.
综上所述, S与t的函数关系式为:
 ;
;
(3)若直线l:y=﹣3x+9t﹣3与⊙M相切,如图所示,应有两条符合条件的切线.
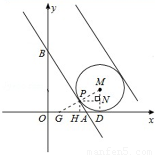
设直线与x轴、y轴交于A、B点,则A(3t﹣1,0)、B(0,9t﹣3),∴OB=3OA.
由题意,可知⊙M与x轴相切,设切点为D,连接MD;
设直线与⊙M的一个切点为P,连接MP并延长交x轴于点G;过P点作PN⊥MD于点N,PH⊥x轴于点H.
易证△PMN∽△BAO,∴PN:MN=OB:OA=3,∴PN=3MN.
在Rt△PMN中,由勾股定理得:PM2=PN2+MN2,解得: MN=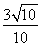 ,PN=
,PN=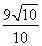 ,
,
∴PH=ND=MD﹣MN=3﹣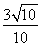 ,OH=OD﹣HD=OD﹣PN=2t+3﹣
,OH=OD﹣HD=OD﹣PN=2t+3﹣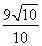 ,
,
∴P(2t+3﹣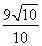 ,3﹣
,3﹣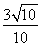 ),代入直线解析式求得:t=5﹣
),代入直线解析式求得:t=5﹣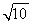 ;
;
同理,当切线位于另外一侧时,可求得:t=5+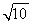 .
.
考点:动点问题.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
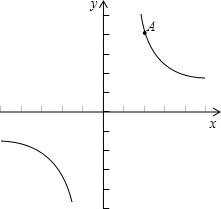
| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=![]() .
.

1.求该反比例函数和一次函数的解析式
2.求△AOC的面积
查看答案和解析>>
科目:初中数学 来源:2010年北京市丰台区中考数学二模试卷(解析版) 题型:解答题
 的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.
的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.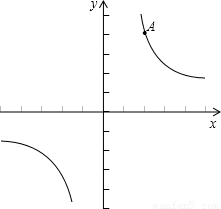
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川巴中卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,一次函数 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出 时x的取值范围。
时x的取值范围。

查看答案和解析>>
科目:初中数学 来源:2013届湖南省八年级反比例函数测试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=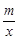 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=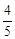 .
.
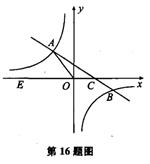
1.求该反比例函数和一次函数的解析式
2.求△AOC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com