
分析 先把x=3,y=3代入y=x2+(a+1)x+b得到b=-3a-9,则利用当x为任意实数时,都有y≥x得到x2+ax-3a-9≥0,则对于抛物线y=x2+ax-3a-9,它与x轴没有公共点或只有一个公共点,根据△的意义得△=(a+6)2≤0,所以a=-6,b=9,于是得到原抛物线解析式为y=x2-5x+9,把它配成顶点式得到顶点坐标,然后根据勾股定理计算抛物线的顶点到原点的距离.
解答 解:把x=3,y=3代入y=x2+(a+1)x+b得9+3a+3+b=3,则b=-3a-9,
∵当x为任意实数时,都有y≥x,
即x2+(a+1)x+b≥x,
∴x2+(a+1)x-3a-9≥x,即x2+ax-3a-9≥0,
∴抛物线y=x2+ax-3a-9与x轴没有公共点或只有一个公共点,
∴△=a2-4(-3a-9)=(a+6)2≤0,
∴a+6=0,解得a=-6,
∴b=9,
∴y=x2-5x+9=(x-$\frac{5}{2}$)2+$\frac{11}{4}$,
∴顶点坐标为($\frac{5}{2}$,$\frac{11}{4}$),
∴抛物线的顶点到原点的距离=$\sqrt{(\frac{5}{2})^{2}+(\frac{11}{4})^{2}}$=$\frac{\sqrt{221}}{4}$.
故答案为$\frac{\sqrt{221}}{4}$.
点评 本题考查了二次根式的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,抛物线上的点满足抛物线解析式.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
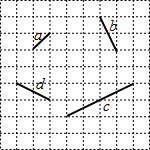 如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )| A. | 3种 | B. | 6种 | C. | 8种 | D. | 12种 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
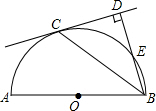 如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
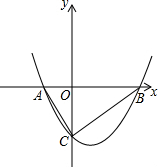 一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.
一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(1+x)2 | B. | a(1+x%)2 | C. | a+a•x% | D. | a+a•(x%)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2与$\sqrt{{{(-2)}^2}}$ | B. | -2和$\root{3}{-8}$ | C. | -$\frac{1}{2}$与2 | D. | |-2|和2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com