
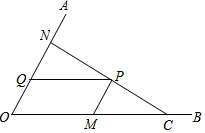
 如图,C为∠AOB的边OB上一点,OC=10,N为边OA上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OB交OA于点Q,PM∥OA交OB于点M.
如图,C为∠AOB的边OB上一点,OC=10,N为边OA上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OB交OA于点Q,PM∥OA交OB于点M.分析 (1)求出CM=4,由平行线证出△MPC∽△ONC,得出$\frac{MP}{ON}=\frac{MC}{OC}$,证出四边形OMPQ为平行四边形,得出PM=OQ=2,代入比例式即可求出ON的长;
(2)设PQ=OQ=x,①证出四边形OQPM是菱形,得出OM=x,MC=10-x,由(1)得:$\frac{MP}{ON}=\frac{MC}{OC}$,得出$\frac{1}{ON}=\frac{10-x}{10x}$,求出$\frac{1}{OM}-\frac{1}{ON}$=$\frac{1}{10}$即可;
②由平行线证出△PMC∽△NOC,△NQP∽△NOC,∴得出$\frac{{S}_{△PMC}}{{S}_{△NOC}}$=$\frac{(10-x)^{2}}{100}$,$\frac{{S}_{△NQP}}{{S}_{△NOC}}$=$\frac{{x}^{2}}{100}$,得出S1=S△NOC-S△PMC-S△NQP=$\frac{-{x}^{2}+10x}{50}$S2,求出$\frac{{S}_{1}}{{S}_{2}}=\frac{-{x}^{2}+10x}{50}$=-$\frac{1}{50}$(x-50)2+$\frac{1}{2}$,即可得出结果.
解答 解:(1)∵OM=6,OC=10,
∴CM=4,
∵MP∥OA,
∴△MPC∽△ONC,
∴$\frac{MP}{ON}=\frac{MC}{OC}$,
∵PQ∥OB,PM∥OA,
∴四边形OMPQ为平行四边形,
∴PM=OQ=2,
∴$\frac{2}{ON}=\frac{4}{10}$,
∴ON=5;
(2)设PQ=OQ=x,
①$\frac{1}{OM}$-$\frac{1}{ON}$的值不发生变化,理由如下:
∵PQ∥OB,PM∥OA,PQ=OQ=x,
∴四边形OQPM是菱形,
∴OM=x,MC=10-x,
由(1)得:$\frac{MP}{ON}=\frac{MC}{OC}$,
∴$\frac{x}{ON}=\frac{10-x}{10}$,
∴$\frac{1}{ON}=\frac{10-x}{10x}$,
∴$\frac{1}{OM}-\frac{1}{ON}$=$\frac{1}{x}$-$\frac{10-x}{10x}$=$\frac{1}{10}$,
∴$\frac{1}{OM}$-$\frac{1}{ON}$的值不发生变化;
②∵PQ∥OB,PM∥OA,
∴△PMC∽△NOC,△NQP∽△NOC,
∴$\frac{{S}_{△PMC}}{{S}_{△NOC}}$=($\frac{MC}{OC}$)2=$\frac{(10-x)^{2}}{100}$,$\frac{{S}_{△NQP}}{{S}_{△NOC}}$=($\frac{QP}{OC}$)2=$\frac{{x}^{2}}{100}$,
∴S1=S△NOC-S△PMC-S△NQP=${S}_{2}-\frac{(10-x)^{2}}{100}{S}_{2}-\frac{{x}^{2}}{100}{S}_{2}$=$\frac{-{x}^{2}+10x}{50}$S2,
∴$\frac{{S}_{1}}{{S}_{2}}=\frac{-{x}^{2}+10x}{50}$=-$\frac{1}{50}$(x-50)2+$\frac{1}{2}$,
∵0<x<10,
∴0<$\frac{{S}_{1}}{{S}_{2}}$≤$\frac{1}{2}$.
点评 此题属于相似形综合题,考查了相似三角形的判定与性质,二次函数的性质,平行四边形的判定与性质,以及菱形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
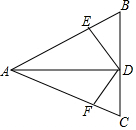 如图所示,在△ABC中,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下列结论:
如图所示,在△ABC中,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
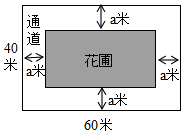 如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com