
如图,正方形ABCD中,P为对角线上的点,PB=AB,连PC,作CE⊥CP交AP的延长线于E,AE交CD于F,交BC的延长线于G,则下列结论:①E为FG的中点;②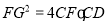 ;③AD=DE;④CF=2DF.其中正确结论的个数是( )
;③AD=DE;④CF=2DF.其中正确结论的个数是( )
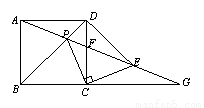
A.1个 B.2个 C.3个 D.4个
C
【解析】
试题分析:①如图:
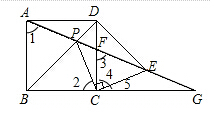
正方形ABCD中BA=BC,∠ABP=∠CBP,BP=BP,∴△ABP≌△CBP,那么∠1=∠2,
在直角三角形ABG中∠1与∠G互余,∠PCE=90°,那么∠2与∠5互余,∴∠5=∠G,∴EC=EG.
在直角三角形FCG中∠3与∠G互余,∠4与∠5也互余,而∠5=∠G,
∴∠3=∠4,∴EC=EF,从而得出EG=EF,即E为FG的中点.∴①正确.
③∵AB=BC,∠ABD=∠CBD,BP=BP,∴△ABP≌△CBP,∴∠1=∠2,∵AB∥CD,∴∠1=∠DFA,
∵AB=BP,∴∠1=∠BPA,∵∠DPF=∠APB,∵EF=CE,∴∠3=∠4,∴∠4=∠DPE,
∴D、P、C、E四点共圆,∴∠DEA=∠DCP,∵∠1+∠DAP=90°,∠2+∠DCP=90°,
∴∠DAP=∠DCP=∠DEA,∴AD=DE,∴③正确,
②∵∠3=∠4,AD=DE(③已求证),∴△CEF∽△CDE,∴ CE:CF=CD:CE 即CE²=CF·CD
∵∠3=∠4,∴CE=EF,∵E为FG的中点.∴FG=2CE,即CE=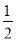 FG,∴
FG,∴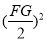 =CF•CD,
=CF•CD,
即FG²=4CF•CD,∴②正确.
④∵四边形ABCD是正方形,∴△PDF∽△PBA,
∴ 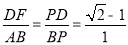 ∴
∴ 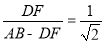 ∴
∴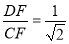 即CF=
即CF=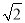 DF∴④错误,
DF∴④错误,
综上所述,正确的由①②③.
故选C.
考点:相似三角形的判定与性质,正方形的性质,勾股定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:填空题
某公司4月份的利润是100万元,要使6月份的利润达到121万元,则平均每月增长的百分率是 。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:解答题
(本小题满分6分)如图二次函数y=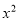 +bx+c的图象经过A(-1,0)和B(3,0)两点,且交
+bx+c的图象经过A(-1,0)和B(3,0)两点,且交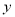 轴于点
轴于点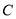 .
.

(1)试确定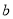 、
、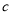 的值;
的值;
(2)过点C作CD∥x轴轴交抛物线于点D点M为此抛物线的顶点,试确定△MCD的形状.
参考公式:顶点坐标(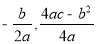 )
)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:填空题
一次函数y=(m+3)x=1若y随x的增大而增大,则m的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:选择题
若关于x的方程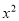 -m=2x有两个不相等的实数根,则m的取值范围是( )
-m=2x有两个不相等的实数根,则m的取值范围是( )
A.m>-1 B.m<-2 C.m≥0 D.m<0
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省九年级上学期期末考试数学试卷(解析版) 题型:解答题
(12分)如图,已知二次函数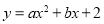 的图像经过A(-1,-1),C(1,3).
的图像经过A(-1,-1),C(1,3).

(1)求二次函数的解析式并画出它的图像;
(2)直接写出点A关于抛物线对称轴的对称点A'的坐标;
(3)求该抛物线上到x轴的距离为2的所有点的坐标.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年河北省九年级上学期期末考试数学试卷(解析版) 题型:选择题
一个密闭不透明的盒子里有若干个白球,在不许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球200次,其中44次摸到黑球,你估计盒中大约有白球( )
A.20个 B.28个 C.36个 D.无法估计
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市新世纪学校七年级上学期期中数学试卷(解析版) 题型:填空题
在数-5,1,-3,5,-2中任选两个数相乘,其中最大的积是________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com