
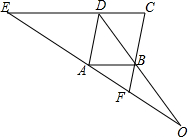
 如图,已知EC∥AB,∠EDA=∠ABF.
如图,已知EC∥AB,∠EDA=∠ABF.分析 (1)由EC∥AB,∠EDA=∠ABF,可证得∠DAB=∠ABF,即可证得AD∥BC,则得四边形ABCD为平行四边形;
(2)由EC∥AB,可得$\frac{OA}{OE}$=$\frac{OB}{OD}$,由AD∥BC,可得$\frac{OB}{OD}$=$\frac{OF}{OA}$,等量代换得出$\frac{OA}{OE}$=$\frac{OF}{OA}$,即OA2=OE•OF.
解答  证明:(1)∵EC∥AB,
证明:(1)∵EC∥AB,
∴∠EDA=∠DAB,
∵∠EDA=∠ABF,
∴∠DAB=∠ABF,
∴AD∥BC,
∵DC∥AB,
∴四边形ABCD为平行四边形;
(2)∵EC∥AB,
∴△OAB∽△OED,
∴$\frac{OA}{OE}$=$\frac{OB}{OD}$,
∵AD∥BC,
∴△OBF∽△ODA,
∴$\frac{OB}{OD}$=$\frac{OF}{OA}$,
∴$\frac{OA}{OE}$=$\frac{OF}{OA}$,
∴OA2=OE•OF.
点评 此题考查了相似三角形的判定与性质,平行四边形的判定,平行线的性质,解题时要注意识图,灵活应用数形结合思想.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
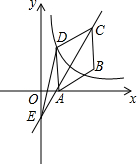 如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=$\frac{k}{x}$(k≠0,x>0)过点D.
如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=$\frac{k}{x}$(k≠0,x>0)过点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对我国初中学生视力状况的调查 | |
| B. | 对量子科学通信卫星上某种零部件的调查 | |
| C. | 对一批节能灯管使用寿命的调查 | |
| D. | 对“最强大脑”节目收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
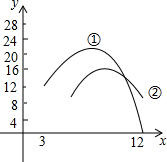 现有一生产季节性产品的企业,有两种营销方案,经测算:方案一一年中获得的每月利润y(万元)和月份x的关系为y=-0.5x2+8x-14,方案二一年中获得的每月利润y(万元)与月份x的关系为y=-x2+14x-24.两个函数部分图象如图所示:
现有一生产季节性产品的企业,有两种营销方案,经测算:方案一一年中获得的每月利润y(万元)和月份x的关系为y=-0.5x2+8x-14,方案二一年中获得的每月利润y(万元)与月份x的关系为y=-x2+14x-24.两个函数部分图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25 | B. | 20 | C. | 15 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com