Question

【题目】如图，矩形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，CB′的长为 ．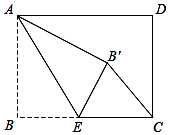

Answer 1

【答案】2或
【解析】解：当△CEB′为直角三角形时，有两种情况：
①当点B′落在矩形内部时，如答图1所示．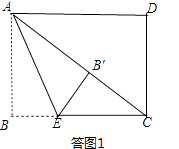

连结AC，在Rt△ABC中，AB=3，BC=4，
∴AC=5，
∵∠B沿AE折叠，使点B落在点B′处，
∴∠AB′E=∠B=90°，
当△CEB′为直角三角形时，只能得到∠EB′C=90°，
∴点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，
∴EB=EB′，AB=AB′=3，
∴CB′=5﹣3=2；
②当点B′落在AD边上时，如答图2所示．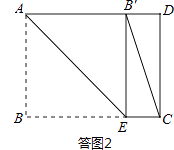

此时ABEB′为正方形，
∴B'E=AB=3，
∴CE=4﹣3=1，
∴Rt△B'CE中，CB'= = ．
综上所述，BE的长为2或 ．
故答案为：2或 ．
当△CEB′为直角三角形时，有两种情况：
①当点B′落在矩形内部时，如答图1所示．
连结AC，先利用勾股定理计算出AC=5，根据折叠的性质得∠AB′E=∠B=90°，而当△CEB′为直角三角形时，只能得到∠EB′C=90°，所以点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，则EB=EB′，AB=AB′=3，可计算出CB′=2，设BE=x，则EB′=x，CE=4﹣x，然后在Rt△CEB′中运用勾股定理可计算出x．
②当点B′落在AD边上时，如答图2所示．此时ABEB′为正方形．