
【题目】如图所示,画一个长和宽分别为![]() 、
、![]() 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.

![]() 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体?
![]() 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件?
【答案】(1)四种不同的圆柱体;(2)旋转轴和旋转角这两个条件.
【解析】
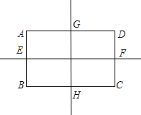
(1)分别以长方形的长和宽所在直线为旋转轴,旋转360°;以对边的中点连线所在直线为旋转轴,旋转180°;
(2)需要说明旋转轴和旋转角这两个条件.
解:![]() 由于长和宽分别为
由于长和宽分别为![]() 、
、![]() 的长方形,旋转可得到四种不同的圆柱体;
的长方形,旋转可得到四种不同的圆柱体;
①一长方形的一条长![]() (或
(或![]() )所在直线为旋转轴,旋转
)所在直线为旋转轴,旋转![]() ,可得到底面半径为
,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;
②一长方形的一条宽![]() (或
(或![]() )所在直线为旋转轴,旋转一周,可得到底面半径为
)所在直线为旋转轴,旋转一周,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;
③以长方形的长![]() 、
、![]() 的中点
的中点![]() 、
、![]() 所在直线为旋转轴,旋转
所在直线为旋转轴,旋转![]() ,可得到底面半径为
,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;
④以长方形的长![]() 、
、![]() 的中点
的中点![]() 、
、![]() 所在直线为旋转轴,旋转
所在直线为旋转轴,旋转![]() ,可得到底面半径为
,可得到底面半径为![]() ,高为
,高为![]() 的圆柱体;
的圆柱体;
![]() 把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.
把一个平面图形旋转成几何体,需要说明旋转轴和旋转角这两个条件.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
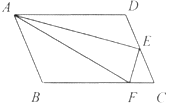
【题目】如图,在□ABCD中,点E是CD的中点,点F是BC边上的一点,且EF⊥AE.求证:AE平分∠DAF.
小林同学读题后有一个想法,延长FE,AD交于点M,要证AE平分∠DAF,只需证△AMF是等腰三角形即可.请你参考小林的想法,完成此题的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个直七棱柱,它的底面边长都是![]() ,侧棱长是
,侧棱长是![]() ,观察这个棱柱,请回答下列问题:
,观察这个棱柱,请回答下列问题:
![]()
![]() 这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出
这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出![]() 棱柱有多少个面?
棱柱有多少个面?
![]() 这个七棱柱一共有多少条棱?它们的长度分别是多少?
这个七棱柱一共有多少条棱?它们的长度分别是多少?
![]() 这个七棱柱一共有多少个顶点?
这个七棱柱一共有多少个顶点?
![]() 通过对棱柱的观察,你能说出
通过对棱柱的观察,你能说出![]() 棱柱的顶点数与
棱柱的顶点数与![]() 的关系及棱的条数与
的关系及棱的条数与![]() 的关系吗?
的关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:在正方形ABCD中,以正方形的一个顶点A为顶点,且过对角顶点C的抛物线,称为这个正方形的以A为顶点的对角抛物线.
(1)在平面直角坐标系xOy中,点在轴正半轴上,点C在y轴正半轴上.
①如图1,正方形OABC的边长为2,求以O为顶点的对角抛物线;
②如图2,在平面直角坐标系xOy中,正方形OABC的边长为a,其以O为顶点的对角抛物线的解析式为y= ![]() x2 , 求a的值;
x2 , 求a的值;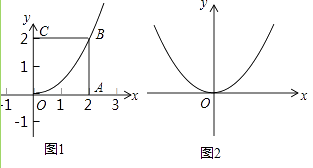
(2)如图3,正方形ABCD的边长为4,且点A的坐标为(3,2),正方形的四条对角抛物线在正方形ABCD内分别交于点M、P、N、Q,直接写出四边形MPNQ的形状和四边形MPNQ的对角线的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数![]() 和y=x的图象于点C,D.
和y=x的图象于点C,D.
(1)求点A的坐标;
(2)若OB=CD,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 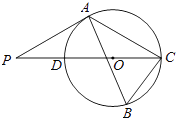
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):
表示立方米):
价目表 | |
每月用水量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注:水费按月结算 | |
例:若某户居民![]() 月份用水
月份用水![]() ,应收水费为
,应收水费为![]() (元).
(元).
请根据上表的内容解答下列问题:
![]() 填空:若该户居民
填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费________元;
,则应收水费________元;
![]() 若该户居民
若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?(用含
),则应收水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
![]() 若该户居民
若该户居民![]() ,
,![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() ,
,![]() 两个月共交水费多少元?(用含
两个月共交水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com