
 OP2,将表示出的OP2代入,可得其面积为关于m的二次函数,其图象开口向上,有最小值,其对称轴为直线x=3
OP2,将表示出的OP2代入,可得其面积为关于m的二次函数,其图象开口向上,有最小值,其对称轴为直线x=3 ,且当0<m≤3
,且当0<m≤3 时,S△OPG随m的增大而减小,利用二次函数的性质即可求出此时S△OPG的最小值;
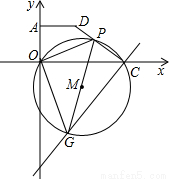
时,S△OPG随m的增大而减小,利用二次函数的性质即可求出此时S△OPG的最小值; OM,表示出OM,又ON为3,利用勾股定理表示出MN2,将(2)得出的OP2代入,得到关于m的二次函数,利用m的范围即可求出n的范围;(ii)当点P在AD边上时,如右图所示,由圆的半径相等得到OM=PM,在直角三角形PDM中,由PD=m-3
OM,表示出OM,又ON为3,利用勾股定理表示出MN2,将(2)得出的OP2代入,得到关于m的二次函数,利用m的范围即可求出n的范围;(ii)当点P在AD边上时,如右图所示,由圆的半径相等得到OM=PM,在直角三角形PDM中,由PD=m-3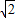 ,DM=3-n,利用勾股定理表示出PM2,在直角三角形OMN中,由ON=3,MN=n,利用勾股定理表示出OM2,两者相等列出关于m与n的关系式,用m表示出n,根据m的范围即可求出n的范围,综上,得到满足题意的n的范围.
,DM=3-n,利用勾股定理表示出PM2,在直角三角形OMN中,由ON=3,MN=n,利用勾股定理表示出OM2,两者相等列出关于m与n的关系式,用m表示出n,根据m的范围即可求出n的范围,综上,得到满足题意的n的范围.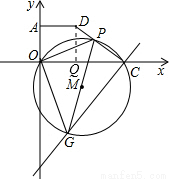 由D(3,3),得到DQ=OQ=3,由C(6,0),得到OC=6,
由D(3,3),得到DQ=OQ=3,由C(6,0),得到OC=6,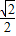 m,
m,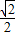 m,PB=
m,PB=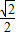 m,
m,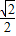 m)2+(6-
m)2+(6-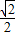 m)2,
m)2, OP•OG=
OP•OG= OP2=
OP2= [(
[(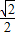 m)2+(6-
m)2+(6-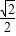 m)2]=
m)2]= (m-3
(m-3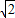 )2+9,
)2+9,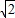 ,
,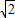 时,S△OPG随m的增大而减小,
时,S△OPG随m的增大而减小,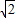 时,S△OPG取得最小值为9;
时,S△OPG取得最小值为9; OC=3,可得直线MN经过点D,连接OM.
OC=3,可得直线MN经过点D,连接OM.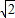 时,如左图可知:∠OPC为钝角或直角,
时,如左图可知:∠OPC为钝角或直角,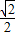 OP,ON=3,又OP2=(
OP,ON=3,又OP2=(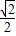 m)2+(6-
m)2+(6-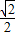 m)2,
m)2,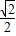 OP)2-32=
OP)2-32= (m-3
(m-3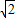 )2+9-9=
)2+9-9= (m-3
(m-3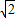 )2,
)2,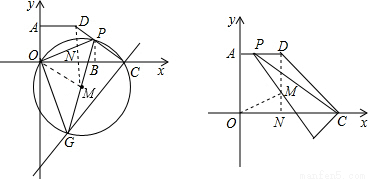 ∵0<m≤3
∵0<m≤3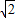 ,
,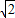 <m≤3
<m≤3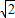 +3时,如右图,依题意得:MO=PM,
+3时,如右图,依题意得:MO=PM,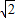 ,
,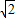 )2,
)2, (m-3
(m-3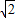 )2,
)2, <m≤3
<m≤3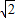 +3,
+3, ,
, .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′. | PP′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 6 |
| x |
| 3 |
| 2 |
| 6 |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:
 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com