Question

11．如图，AD∥BC，AB=AD=DC，∠ABC=∠DCB，点E、F分别为DC、BC上一动点，且满足∠EAF=$\frac{1}{2}$∠BAD，EG∥BC交AF于G．探究线段DE、BF和GE的数量关系．

Answer 1

分析 延长CB，截取BM=DE，连接AM、EF，由平行线的性质和已知条件得出∠D=∠ABM，由SAS证明△ABM≌△ADE，得出∠BAM=∠DAE，AM=AE，证出∠MAF=∠EAF，由SAS证明△AEF≌△AMF，得出EF=MF=DE+BF，∠AFE=∠AFM，由平行线的性质证出∠EFA=∠EGF，得出EG=EF，即可得出结论．

解答 解：DE+BF=GE；理由如下：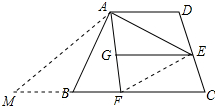
延长CB，截取BM=DE，连接AM、EF，如图所示：
∵AD∥BC，
∴∠DCB+∠D=180°，
∵∠ABC=∠DCB，
∴∠ABC+∠D=180°，
∵∠ABC+∠ABM=180°，
∴∠D=∠ABM，
在△ABM和△ADE中，$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠ABM=∠D}&{\;}\\{BM=DE}&{\;}\end{array}\right.$，
∴△ABM≌△ADE（SAS），
∴∠BAM=∠DAE，AM=AE，
∵∠EAF=$\frac{1}{2}$∠BAD，
∴∠DAE+∠BAF=∠EAF，
∴∠BAF+∠BAM=∠EAF，
∴∠MAF=∠EAF，
在△AEF和△AMF中，$\left\{\begin{array}{l}{AE=AM}&{\;}\\{∠EAF=∠MAF}&{\;}\\{AF=AF}&{\;}\end{array}\right.$，
∴△AEF≌△AMF（SAS），
∴EF=MF=DE+BF，∠AFE=∠AFM，
∵EG∥BC，
∴∠EGF=∠AFM，
∴∠EFA=∠EGF，
∴GE=EF，
∴DE+BF=GE．

点评 本题考查了全等三角形的判定与性质、梯形的性质、等腰三角形的判定与性质等知识；本题综合性强，有一定难度，需要通过作辅助线两次证明三角形全等才能得出结论．