练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1、如图所示，在△ABD和△ACE中，有下列四个论断：①AB=AC，②AD=AE  ③∠B=∠C，④BD=CE．
    请以其中三个论断作为条件，余下一下作为结论，写出一个正确的数学题（用序号表示）
    由①②④ ?③或①③④ ?②，
    并证明．
    分析：本题的题意是先证三角形全等，然后得出简单的角或边相等．根据全等三角形的判定定理可知：
    ①②④?③是根据SSS来判定其全等，从而得到全等三角形的对应角相等．
    ①③④?②是根据SAS来判定其全等，从而得到全等三角形的对应边相等．
    解答：解：由①②④?③或①③④?②；
    先证前一种：
    ∵AB=AC，AD=AE，BD=CE，
    ∴△ABD≌△ACE（SSS）；
    ∴∠B=∠C；
    再证第二种：
    ∵AB=AC，∠B=∠C，BD=CE，
    ∴△ABD≌△ACE（SAS）；
    ∴AD=AE．
    点评：此题主要考查全等三角形的判定方法，常用的判定方法有SAS、SSS、AAS、ASA、HL等，要求学生对常用的这几种判定方法要熟练掌握．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

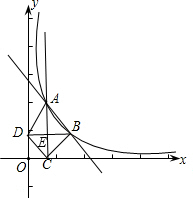    精英家教网如图所示，在直角坐标系平面内，函数y=
    m
    x
    （x＞0，m是常数）的图象经过A（1，4），B（a、b）其中a＞1，过点A作x轴的垂线，垂足为C，过点B作y轴的垂线，垂足为D，连接AD，DC，CB且BD，AC交于点E．
    （1）用含a的代数式表示E点的坐标；
    （2）若△ABD的面积是4，求点B的坐标；
    （3）当CD=
    5
    3
    时，求点B的坐标；
    （4）求△ADE的面积与△CBE的面积的比值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•邵阳）如图所示，在Rt△ABC中，AB=BC=4，∠ABC=90°，点P是△ABC的外角∠BCN的角平分线上一个动点，点P′是点P关于直线BC的对称点，连结PP′交BC于点M，BP′交AC于D，连结BP、AP′、CP′．
    （1）若四边形BPCP′为菱形，求BM的长；
    （2）若△BMP′∽△ABC，求BM的长；
    （3）若△ABD为等腰三角形，求△ABD的面积．

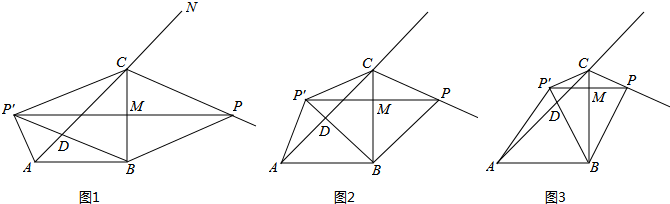
    查看答案和解析>>

    科目：初中数学 来源：黄冈难点课课练　　七年级数学下册(北师大版) 题型：022

    如图所示，在△ABD与△ACE中，有下列四个论断：①AB＝AC；②AD＝AE；③∠B＝∠C；④BD＝CE．请以其中三个论断作为条件，余下一个论断作为结论，写出一个正确的命题________．(用序号→的形式写出)

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

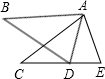    如图所示，在△ABD和△ACE中，有下列四个论断：①AB=AC，②AD=AE　③∠B=∠C，④BD=CE．
    请以其中三个论断作为条件，余下一下作为结论，写出一个正确的数学题（用序号表示）________并证明．

    查看答案和解析>>

    同步练习册答案