
【题目】如图,直线y= ![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )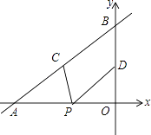
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
【答案】C
【解析】解:(方法一)作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
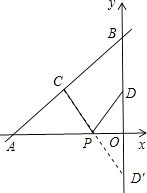
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(﹣3,2),D′(0,﹣2),
∴有 ![]() ,解得:
,解得: 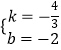 ,
,
∴直线CD′的解析式为y=﹣ ![]() x﹣2.
x﹣2.
令y=﹣ ![]() x﹣2中y=0,则0=﹣
x﹣2中y=0,则0=﹣ ![]() x﹣2,解得:x=﹣
x﹣2,解得:x=﹣ ![]() ,
,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.
(方法二)连接CD,作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
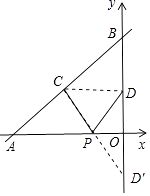
令y= ![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y= ![]() x+4中y=0,则
x+4中y=0,则 ![]() x+4=0,解得:x=﹣6,
x+4=0,解得:x=﹣6,
∴点A的坐标为(﹣6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(﹣3,2),点D(0,2),CD∥x轴,
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,﹣2),点O为线段DD′的中点.
又∵OP∥CD,
∴点P为线段CD′的中点,
∴点P的坐标为(﹣ ![]() ,0).
,0).
故选C.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.a,b,c是直线,且a∥b,b∥c,则a∥c
B.a,b,c是直线,且a⊥b,b⊥c,则a⊥c
C.a,b,c是直线,且a∥b,b⊥c,则a∥c
D.a,b,c是直线,且a∥b,b∥c,则a⊥c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“日啖荔枝三百颗,不辞长作岭南人”,广东的夏季盛产荔枝,桂味、糯米糍是荔枝的品种之一.佳佳同学先用52元购买2千克桂味和1千克糯米糍;几天后,他用76元购买1千克桂味和3千克糯米糍.(前后两次两种荔枝的售价不变)
(1)求桂味、糯米糍的售价分别是每千克多少元?
(2)若佳佳同学用y元买了这两种荔枝共中10千克,设买了x千克桂味. ①写出y与x的函数关系式.
②若要求糯米糍的重量不少于桂味重量的3倍,请帮佳佳同学设计一个购买方案,使所需的费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
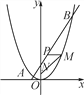
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳今年4月份某星期的最高气温如下(单位℃):26,25,27,28,27,25,25,则这个星期的最高气温的众数和中位数分别是( )
A.25,26B.25,26.5C.27,26D.25,28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米,将2500000用科学记数法表示应为( )平方千米.
A.250×104
B.25×105
C.2.5×106
D.0.25×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣2x+a与y轴交于点C (0,6),与x轴交于点B. 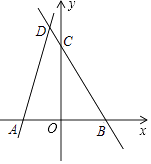
(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(﹣1,n),点A的坐标为(﹣3,0). ①求n的值及直线AD的解析式;
②求△ABD的面积;
③点M是直线y=﹣2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com