
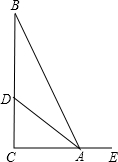
 如图,在△ABC中,∠C=90°,AD平分∠BAC,∠ADC=66°,E为CA延长线上一点.试求∠BAE的度数.
如图,在△ABC中,∠C=90°,AD平分∠BAC,∠ADC=66°,E为CA延长线上一点.试求∠BAE的度数.  同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在一次暴风雨后,一棵大树从离地面3m处被折断,经测量树的顶端与地面的接触点离树根部的距离为2m,若在该树正上方离地面7m处有高压电线l,请判断,该树在折断前是否接触到电线?并说明你的理由.
如图所示,在一次暴风雨后,一棵大树从离地面3m处被折断,经测量树的顶端与地面的接触点离树根部的距离为2m,若在该树正上方离地面7m处有高压电线l,请判断,该树在折断前是否接触到电线?并说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com