不定方程a2+b2+c2=a2b2的所有整数解是 .
【答案】
分析:首先对其中c进行分析,c等于零 奇数 偶数再对a b分析(同为奇数 偶数 一奇一偶),求出每种情况的解的情况,再依次进行分析,最终求出方程的解.只有一个解.
解答:解:首先对c进行奇偶性分析:
(1)c=0时,方程化为a
2+b
2=a
2b
2,即(a
2-1)(b
2-1)=1由于a
2-1与b
2-1都是1的约数,
所以
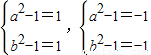
以上方程组只能解出a=b=0,于是,方程有一组解a=b=c=0.
(2)c为奇数时,再对a,b进行奇偶性分析.
(i)若a和b同为奇数,则a
2,b
2,c
2都是4k+1型,于是a
2+b
2+c
2为4k+3型,而a
2b
2为4k+1型,等式不能成立,方程无解;
(ii)若a,b同为偶数,此时方程左边=a
2+b
2+c
2为奇数,左边=a
2b
2为偶数,方程无解;
(iii)若a和b为一奇一偶,此时方程左边为4k+2型,右边为4k时,方程无解.
(3)c为偶数时,仍对a和b进行奇偶性分析:
(i)若a和b同为奇数,则方程左边为4k+2型,右边为奇数,方程无解;
(ii)若a和b为一奇一偶,则方程左边为奇数,右边为偶数,方程无解;
(iii)若a,b同为偶数,这时,方程两边均为4k型,需要再细致分析:
设a=2
mα,b=2
nβ,c=2
tr,其中m,n,t为非负整数,α,β,r为奇数.则方程化为2
2mα
2+2
2nβ
2+2
2tr
2=2
2m+2nα
2β
2当t最小时,方程两边约去2
2t,得2
2m-2tα
2+2
2n-2tβ
2+r
2=α
2β
2•2
2m+2n-2t显然,方程左边为奇数,右边为偶数,方程无解;
当m最小时,方程两边约去2
2m得α
2+2
2n-2mβ
2+2
2t-2mr
2=2
2nα
2β
2.
同样,方程左边为奇数,右边为偶数,方程无解;
当n最小时,同样可得方程无解.
当m=n=t时,则方程左边是奇数,而右边是偶数,方程无解;
综上讨论,方程a
2+b
2+c
2=a
2b
2只有一组整数解a=0,b=0,c=0.
点评:解此题的关键是如何对abc进行分析,分析要全面(如奇数偶数零),求出所有情况的方程的解,再针对所有的进行归纳和总结.

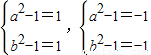 以上方程组只能解出a=b=0,于是,方程有一组解a=b=c=0.
以上方程组只能解出a=b=0,于是,方程有一组解a=b=c=0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案