
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.

【答案】(1)证明见解析;(2)BE∥DF,理由见解析.
【解析】
试题分析:(1)先证∠AED=∠CGD,再证明△ADE≌△CDG,根据全等三角形的对应边相等即可得出结论;
(2)先证明△AEB≌△CGD,得出对应角相等∠AEB=∠CGD,得出∠AEB=∠EGF,即可证出平行线.
试题解析:(1)在正方形ABCD中,
∵AD=CD,
∴∠DAE=∠DCG,
∵DE=DG,
∴∠DEG=∠DGE,
∴∠AED=∠CGD.
在△AED和△CGD中,
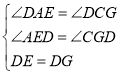
∴△AED≌△CGD(AAS),
∴AE=CG.
(2)BE∥DF,理由如下:
在正方形ABCD中,AB∥CD,
∴∠BAE=∠DCG.
在△AEB和△CGD中,

∴△AEB≌△CGD(SAS),
∴∠AEB=∠CGD.
∵∠CGD=∠EGF,
∴∠AEB=∠EGF,
∴BE∥DF.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】下列结论:
①数轴上的点只能表示有理数;
②任何一个无理数都能用数轴上的点表示;
③实数与数轴上的点一一对应;
④有理数有无限个,无理数有有限个.
其中,正确的结论有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
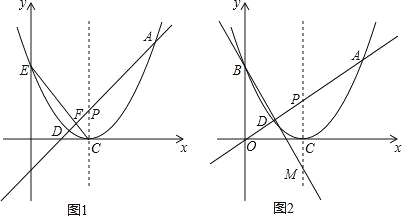
【题目】如图,在平面直角坐标系xOy中,抛物线y=![]() x2-3x+
x2-3x+![]() 交y轴于点E,C为抛物线的顶点,直线AD:y=kx+b(k>0)与抛物线相交于A,D两点(点D在点A的下方).
交y轴于点E,C为抛物线的顶点,直线AD:y=kx+b(k>0)与抛物线相交于A,D两点(点D在点A的下方).
(1)当k=2,b=-3![]() 时,求A,D两点坐标;
时,求A,D两点坐标;
(2)当b=2-3k时,直线AD交抛物线的对称轴于点P,交线段CE于点F,求![]() 的最小值;
的最小值;
(3)当b=0时,若B是抛物线上点A的对称点,直线BD交对称轴于点M,求证:PC=CM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,a所表示的点总在b所表示的点的右边,且|a|=6,|b|=3,则a-b的值为( )
A. -3 B. -9 C. -3或-9 D. 3或9
查看答案和解析>>
科目:初中数学 来源: 题型:
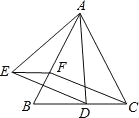
【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com