Question

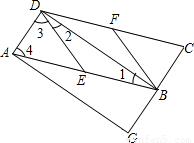
已知如图在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥BD交CB的延长线于G.

（1）求证：△ADE≌△CBF；

（2）若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论。

 

Answer 1

【答案】

（1）证明：∵四边形ABCD是平行四边形，

∴∠4=∠C，AD=CB，AB=CD．

∵点E、F分别是AB、CD的中点，

∴AE=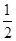AB，CF=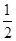CD．

∴AE=CF．

∴△ADE≌△CBF（SAS）．

（2）解：当四边形BEDF是菱形时，四边形AGBD是矩形．

证明：∵四边形ABCD是平行四边形，

∴AD∥BC．

∵AG∥BD，

∴四边形AGBD是平行四边形．

∵四边形BEDF是菱形，

∴DE=BE．

∵AE=BE，

∴AE=BE=DE．

∴∠1=∠2，∠3=∠4．

∵∠1+∠2+∠3+∠4=180°，

∴2∠2+2∠3=180°．

∴∠2+∠3=90°．

即∠ADB=90°．

∴四边形AGBD是矩形．

【解析】（1）在证明全等时常根据已知条件，分析还缺什么条件，然后用（SAS，ASA，SSS）来证明全等；

（2）先由菱形的性质得出AE=BE=DE，再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°，所以判定四边形AGBD是矩形．