
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
【答案】
(1)解:设A种商品的单价为x元、B种商品的单价为y元,由题意得:
![]() ,
,
解得 ![]() .
.
答:A种商品的单价为16元、B种商品的单价为4元
(2)解:设购买A商品的件数为m件,则购买B商品的件数为(2m﹣4)件,由题意得:
![]() ,
,
解得:12≤m≤13,
∵m是整数,
∴m=12或13,
故有如下两种方案:
方案(1):m=12,2m﹣4=20 即购买A商品的件数为12件,则购买B商品的件数为20件;
方案(2):m=13,2m﹣4=22 即购买A商品的件数为13件,则购买B商品的件数为22件.
【解析】(1)设A种商品的单价为x元、B种商品的单价为y元,根据等量关系:①购买60件A商品的钱数+30件B商品的钱数=1080元,②购买50件A商品的钱数+20件B商品的钱数=880元分别列出方程,联立求解即可.(2)设购买A商品的件数为m件,则购买B商品的件数为(2m﹣4)件,根据不等关系:①购买A、B两种商品的总件数不少于32件,②购买的A、B两种商品的总费用不超过296元可分别列出不等式,联立求解可得出m的取值范围,进而讨论各方案即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个熟练的采茶工,一天工作10个小时能采4﹣5万个牙尖,需要两天时间才能采到制500克纯芽的茶青.500克信阳纯芽毛尖干茶需要大约9万个茶芽制成,一片茶芽大约0.00556克.请将0.00556用科学记数法表示为( )
A. 55.6×10﹣4B. 5.56×10﹣3C. 5.56×103D. 0.55×10﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一支原长为20cm的蜡烛,点燃后,其剩余长度y(cm)与燃烧时间x(min)之前的关系如表:
燃烧时间x(min) | 10 | 20 | 30 | 40 | 50 | … |
剩余长度y(cm) | 19 | 18 | 17 | 16 | 15 | … |
(1)表中反映的自变量是什么?因变量是什么?
(2)求出剩余长度y(cm)与燃烧时间x(min)之间的关系式;
(3)估计这支蜡烛最多可燃烧多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒. 
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
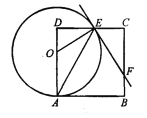
【题目】如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于 点F,且∠CEF=2∠DAE.
(1)求证:直线EF为⊙O的切线;
(2)在点O的运动过程中,设DE=x,解决下列问题:
①求OD·CF的最大值,并求此时半径的长;
②试猜想并证明△CEF的周长为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知二次函数的解析式是y=ax2+bx(a>0),顶点为A(1,-1).
(1)a= ;
(2)若点P在对称轴右侧的二次函数图像上运动,连结OP,交对称轴于点B,点B关于顶点A的对称点为C,连接PC、OC,求证:∠PCB=∠OCB;
(3)如图②,将抛物线沿直线y=-x作n次平移(n为正整数,n≤12),顶点分别为A1,A2,…,An,横坐标依次为1,2,…,n,各抛物线的对称轴与x轴的交点分别为D1,D2,…,Dn,以线段AnDn为边向右作正方形AnDnEnFn,是否存在点Fn恰好落在其中的一个抛物线上,若存在,求出所有满足条件的正方形边长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com